|
14.1.3空间向量的基本定理<-->14.2.1空间直角坐标系
空间向量数量积运算
Ⅰ、空间向量数量积的概念:
⑴概念:已知两个非零向量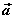 与 与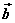 ,我们把数量 ,我们把数量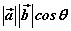 叫做 叫做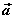 与 与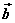 的数量积(或内积)。记作 的数量积(或内积)。记作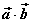 ,即 ,即
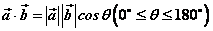 。 。
其中θ是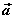 与 与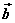 的夹角,向量夹角的范围是0°≤θ≤180°。 的夹角,向量夹角的范围是0°≤θ≤180°。
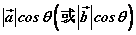 叫做向量 叫做向量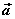 在 在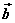 方向上(或 方向上(或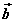 在 在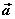 方向上)的投影。 方向上)的投影。
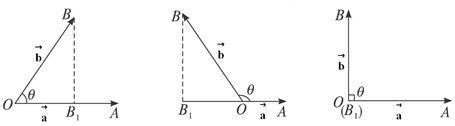
如图为两向量数量积的各种关系:
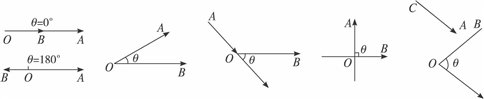
⑵概念说明:
1o 零向量与任一向量的数量积为0,即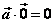 。 。
2o 符号“·”在向量运算中不是乘号,既不能省略,也不能用“ ”代替。 ”代替。
3o 当0≤θ<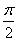 时,cosθ>0,从而 时,cosθ>0,从而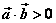 ;当 ;当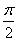 <θ≤π时,cosθ<0,从而 <θ≤π时,cosθ<0,从而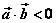 ;当θ= ;当θ=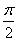 时,cosθ=0,从而 时,cosθ=0,从而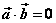 。 。
Ⅱ、空间向量数量积的几何意义:
向量的数量积的几何意义为数量积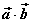 等于 等于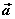 的长度与 的长度与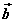 在 在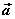 方向上投影 方向上投影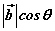 的乘积。 的乘积。
Ⅲ、空间向量数量积的运算性质:
设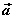 、 、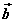 为两个非零向量, 为两个非零向量,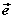 是与 是与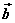 同向的单位向量,则 同向的单位向量,则
⑴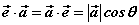 ; ;
⑵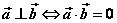 ; ;
⑶当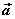 与 与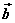 同向时, 同向时,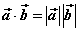 ;当 ;当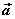 与 与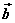 反向时, 反向时,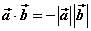 ; ;
特别地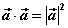 或 或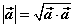 ; ;
⑷ 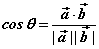 ; ;
⑸ 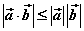 。 。
Ⅳ、空间向量数量积的运算律:
设向量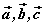 和实数λ,则向量的数量积满足下列运算律: 和实数λ,则向量的数量积满足下列运算律:
⑴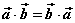 (交换律); (交换律);
⑵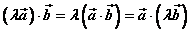 (数乘结合律); (数乘结合律);
⑶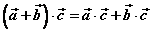 (分配律)。 (分配律)。
Ⅴ、空间向量数量积的坐标表示:
设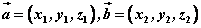 ,则 ,则
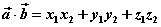 。 。
即两个向量的数量积等于它们对应坐标的乘积的和。
空间向量数量积运算的应用
⑴求证垂直:求证两直线垂直转化为求证两直线的方向向量垂直。
若设两直线的方向向量分别为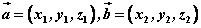 ,则 ,则
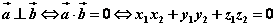
⑵求向量的模:若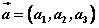 ,则 ,则
 。 。
⑶求两直线的夹角:求两直线的夹角转化为求两直线的方向向量的夹角。
若设两直线的方向向量分别为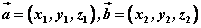 ,则 ,则
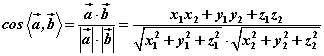 。 。
⑷求两点间的距离:求两点间的距离转化为求以这两点为始终点的有向线段的长度,即求向量的模。
若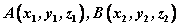 ,则 ,则
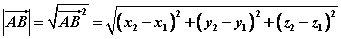 。 。
⑸求平面的法向量:
1o 平面的法向量:如果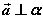 ,那么向量 ,那么向量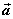 叫做平面 叫做平面 的法向量。 的法向量。
2o 求平面的法向量:
设非零向量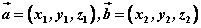 ,使得 ,使得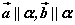 , ,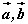 不共线,若非零向量 不共线,若非零向量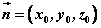 为平面 为平面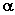 的法向量,则 的法向量,则
 。 。
解得 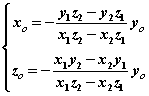 , ,
令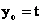 ( (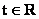 , ,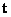 可取使 可取使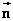 尽量简单的常数值),则法向量 尽量简单的常数值),则法向量
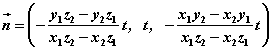 。 。
⑹求空间点面距离:
如图,设平面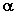 的法向量 的法向量 及平面 及平面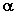 上一点A,则点P到 上一点A,则点P到
平面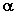 的距离d为 的距离d为
 。 。
用向量方法求点面距离的特点是不要作垂线,不要求找到垂足就可以求得点面距离。
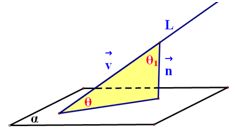
⑺求线面所成的角:
设直线L的方向向量为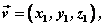 平面 平面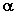 的法向量为 的法向量为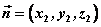 ,向量 ,向量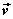 与 与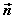 的夹角为 的夹角为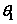 ,直线L与平面 ,直线L与平面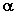 所成的角为 所成的角为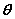 ,则 ,则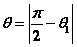 , ,
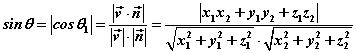 。 。
⑻求空间二面角:
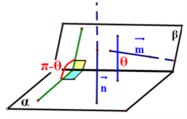
设平面α的法向量为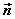 ,平面β的法向量为 ,平面β的法向量为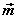 ,向量 ,向量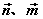 所成的角为 所成的角为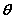 , ,
若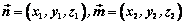 , ,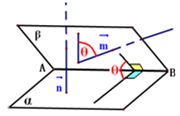
则
 。 。
那么二面角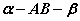 的大小为 的大小为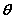 或 或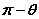 ,视具体情况而定(如图)。 ,视具体情况而定(如图)。
14.1.3空间向量的基本定理<-->14.2.1空间直角坐标系
全网搜索"14.1.4空间向量的数量积"相关
|

