|
返回列表<-->14.1.2共线向量和共面向量
空间向量的概念
①向量定义:一般地,既有大小,又有方向的量叫做向量。
②相关概念:
Ⅰ、向量的模: 向量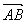 (或 (或 )的大小,就是向量 )的大小,就是向量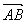 (或 (或 )的长度,称为向量的模,记作| )的长度,称为向量的模,记作|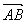 |(或 |(或 )。 )。
向量与向量的模的概念表明,向量不能比大小,向量的模可以比较大小。
Ⅱ、零向量与单位向量:
长度为0的向量叫零向量,记作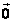 。规定零向量的方向是任意的。 。规定零向量的方向是任意的。
长度为1个单位长度的向量,叫单位向量,记作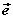 。 。
概念表明,零向量、单位向量的定义都只是限制了大小,而没确定的方向。
Ⅲ、相等向量、平行向量和共线向量:
⑴相等向量:长度相等且方向相同的向量叫做相等向量。
⑵平行向量:方向相同或相反的非零向量叫做平行向量。向量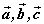 平行,记作 平行,记作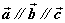 。 。
规定零向量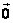 与任一向量平行,即 与任一向量平行,即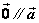 。 。
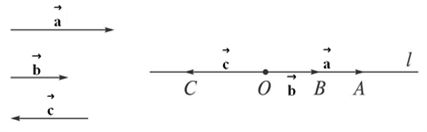
⑶共线向量:平行向量也叫做共线向量。因此,共线向量就是平行向量,平行向量就是共线向量。
⑷区别与联系:相等向量一定是平行向量,也一定是共线向量;反之,平行向量、共线向量不一定是相等向量。平行向量可以在同一条直线上,共线向量可以不在同一条直线上。
空间向量的表示
①有向线段:具有方向的线段就叫做有向线段。它有三个要素:起点、方向、长度。
②空间向量的表示:
Ⅰ、空间向量的几何表示:
⑴用“有向线段”表示。记作 。 。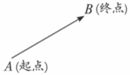
⑵向量与有向线段的区别:有向线段只是向量的一种几何表示,不能说“向量就是有向线段,有向线段就是向量”。因为向量只由方向和大小决定,而与向量起点的位置无关,但有向线段不仅与方向、长度有关,且与起点的位置有关。
Ⅱ、空间向量的字母表示:
⑴可用字母a,b,c,…表示,若印刷用粗黑体字母表示,若手写,则用字母a 头上加“→”来表示,如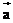 ,手写体上面的箭头一定不能漏写。 ,手写体上面的箭头一定不能漏写。
⑵可以用表示向量的有向线段的起点和终点字母表示,如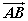 、 、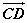 。 。
Ⅲ、空间向量的坐标表示:
在空间直角坐标系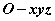 中,对空间任一点 中,对空间任一点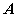 ,存在唯一的有序实数组 ,存在唯一的有序实数组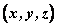 ,使 ,使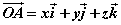 ,有序实数组 ,有序实数组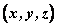 叫作向量 叫作向量 (或 (或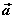 )在空间直角坐标系 )在空间直角坐标系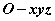 中的坐标,记作 中的坐标,记作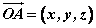 (或 (或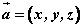 ), ),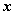 叫横坐标, 叫横坐标, 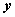 叫纵坐标, 叫纵坐标,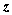 叫竖坐标。 叫竖坐标。
显然,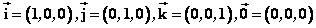 。 。
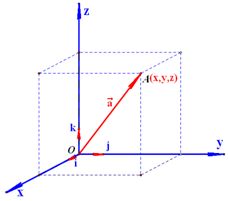
空间向量的加法运算:
(1)空间向量加法运算的定义:
如图,已知非零向量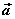 、 、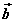 ,在空间内任取一点A,作 ,在空间内任取一点A,作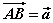 , ,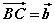 ,则向量 ,则向量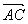 叫做向量 叫做向量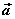 与 与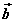 的和,记作 的和,记作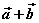 ,即 ,即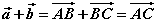 。 。
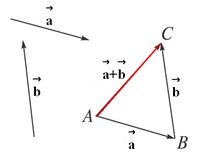
求两个向量和的运算,叫做向量的加法。
⑵空间向量加法运算的几何意义:
1°向量加法的三角形法则:
向量加法定义给出的求向量和的方法就是向量加法的三角形法则。运用这一法则时,要特别注意“首尾相接”,即第二个向量要以第一个向量的终点为起点,则由第一个向量的起点指向第二个向量的终点的向量即为和向量。
2°向量加法的平行四边形法则:
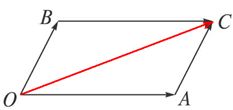
如图,以同一点O为起点的两个已知向量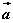 、 、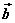 为邻边作平行四边形,则以O为起点的对角线 为邻边作平行四边形,则以O为起点的对角线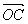 就是向量 就是向量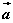 与 与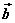 的和。我们把这种作两个向量和的方法叫做向量加法的平行四边形法则。 的和。我们把这种作两个向量和的方法叫做向量加法的平行四边形法则。
⑶空间向量加法运算律:
1o 加法交换律: 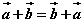 。 。
2o 加法结合律: 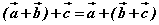 。 。
空间向量的减法运算
⑴空间向量减法运算的定义:
1o 相反向量:规定与向量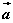 长度相等,方向相反的向量,叫做向量 长度相等,方向相反的向量,叫做向量 的相反向量,记作 的相反向量,记作 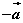 。 。
规定:零向量的相反向量是零向量。
2o 空间向量减法运算的定义:规定
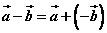 。 。
即减去一个向量相当于加上这个向量的相反向量。
⑵空间向量的减法运算的几何意义:
1°向量减法的平行四边形法则:
如图,已知向量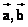 ,作向量 ,作向量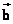 的相反向量 的相反向量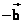 ,以空间一点O为起点, ,以空间一点O为起点,
以两个向量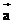 、 、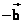 为邻边作平行四边形OACD,则以O为起点的对角线 为邻边作平行四边形OACD,则以O为起点的对角线
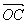 就是向量 就是向量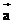 与 与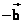 的和,实质上就是向量 的和,实质上就是向量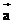 与 与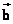 的差。这种作两个向量差 的差。这种作两个向量差
的方法叫做向量减法的平行四边形法则。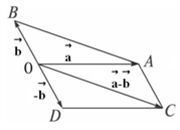
2°向量减法的三角形法则: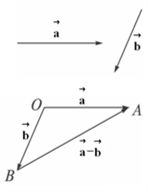
如图,已知向量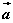 、 、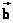 ,在空间内任取一点O,作 ,在空间内任取一点O,作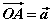 , ,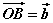 , ,
则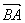 = =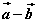 ,即向量 ,即向量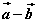 可以表示为从向量 可以表示为从向量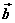 的终点指向向量 的终点指向向量 的终点 的终点
的向量,这就是向量减法的几何意义,也就是向量减法的三角形法则。
⑶空间向量加减运算的坐标表示:
已知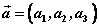 , ,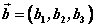 ,则 ,则
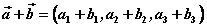 , ,
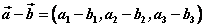 。 。
即两个向量和(差)的坐标分别等于这两个向量相应坐标的和(差)。
空间向量的数乘运算
⑴空间向量数乘运算定义:
我们规定实数λ与向量 的积是一个向量,这种运算叫做向量的数乘,记作 的积是一个向量,这种运算叫做向量的数乘,记作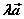 。它的长度与方向规定如下: 。它的长度与方向规定如下:
1o 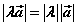 ; ;
2o 当λ>0时,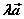 的方向与 的方向与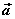 的方向相同;当λ<0时, 的方向相同;当λ<0时,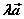 的方向与 的方向与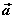 的方向相反;当λ=0时, 的方向相反;当λ=0时,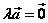 。 。
⑵空间向量数乘运算的几何意义:平面向量数乘运算的几何意义是把向量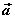 沿 沿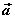 的方向或 的方向或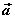 的反方向放大或缩小。 的反方向放大或缩小。
⑶空间向量数乘运算律:
设λ、μ为实数,那么
1o 对实数的结合律:  ; ;
2o 对实数加法的分配率: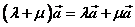 ; ;
3o 对向量加法的分配率: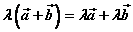 。 。
⑷空间向量共线定理:如果向量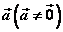 与 与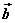 共线(或说 共线(或说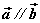 ),那么有且只有一个实数λ,使 ),那么有且只有一个实数λ,使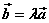 。 。
⑸直线的方向向量:如果向量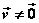 与直线 与直线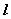 平行,则称向量 平行,则称向量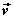 为直线 为直线 的方向向量。 的方向向量。
⑹空间向量数乘运算的坐标表示:
若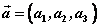 ,则 ,则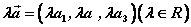 。 。
即实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
返回列表<-->14.1.2共线向量和共面向量
全网搜索"14.1.1空间向量及其加减法与数乘运算"相关
|

