|
12.3.4抛物线的焦点弦的性质<-->12.4.1直线与圆锥曲线的位置关系
抛物线与点的位置关系
Ⅰ、抛物线与点的位置关系:
对于抛物线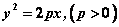 而言,已知点 而言,已知点 。 。
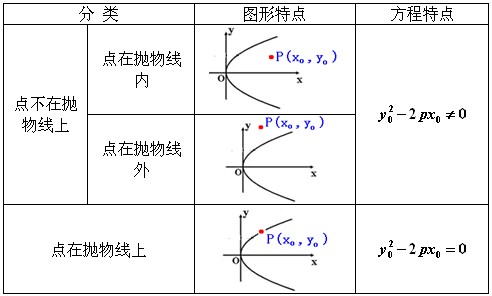
Ⅱ、判断方法:
(1)“以点代面”判断法:即在抛物线外找一特殊的点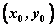 ,将其坐标代入抛物线方程 ,将其坐标代入抛物线方程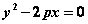 的左边式子,得 的左边式子,得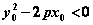 或 或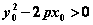 则判断出 则判断出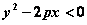 或 或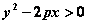 的点与点 的点与点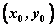 在同一区域内。 在同一区域内。
(2)“关系结论”判断法:
对于抛物线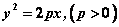 而言,已知点 而言,已知点 , ,
若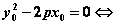 则点 则点 在抛物线上; 在抛物线上;
若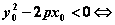 则点 则点 在抛物线内; 在抛物线内;
若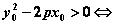 则点 则点 在抛物线外。 在抛物线外。
抛物线与直线的位置关系
Ⅰ、抛物线与直线的位置关系:
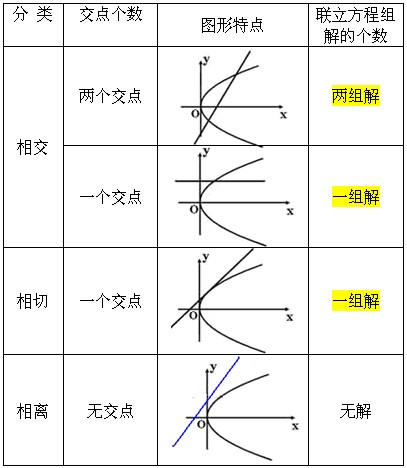
Ⅱ、抛物线与直线位置关系的判断:
已知抛物线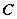 ; ;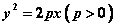 ,直线 ,直线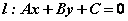 ,联立得 ,联立得
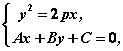 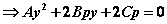 , ,
1o 若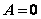 ,则方程组有唯一一组解 ,则方程组有唯一一组解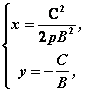 抛物线与直线相交于一点; 抛物线与直线相交于一点;
2o 若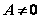 ,则 ,则 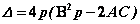 , ,
当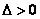 时,抛物线与直线相交于两点;当 时,抛物线与直线相交于两点;当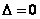 时,抛物线与直线相切于一点;当 时,抛物线与直线相切于一点;当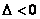 时,抛物线与直线不相交,即相离。 时,抛物线与直线不相交,即相离。
Ⅲ、抛物线与直线位置关系的特点研究:
1o 抛物线与直线相交于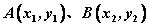 两点,若直线的斜率为 两点,若直线的斜率为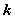 ,则弦长 ,则弦长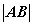 为 为
 。 。
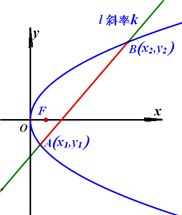 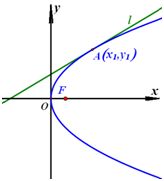
2o 抛物线与直线相切于点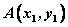 ,若抛物线方程是 ,若抛物线方程是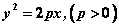 , ,
则已知切点的抛物线切线方程为
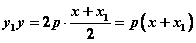 。 。
此外,求抛物线切线方程的一般方法是:“联立—消元—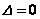 ”。 ”。
3o 抛物线与直线相离,则可求抛物线与直线距离最近的点,或直线与抛物线最短的距离。
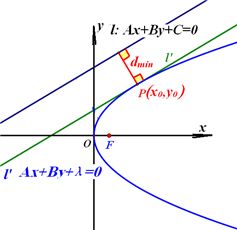
设抛物线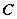 ; ;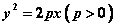 ,直线 ,直线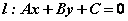 。 。
方法1:如图, 是抛物线上任意一点,求点 是抛物线上任意一点,求点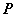 到直线 到直线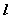 的距离最小值,这最小值就是直线与抛物线的最短距离。即求 的距离最小值,这最小值就是直线与抛物线的最短距离。即求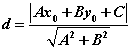 的最小值。 的最小值。
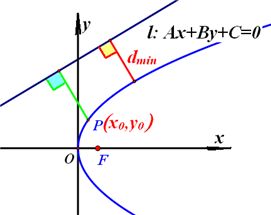
方法2:如图,平行于直线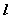 的动直线 的动直线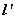 : :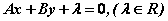 与抛物线 与抛物线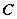 相切时,平行线 相切时,平行线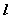 与 与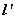 之间的距离就是直线与抛物线的最短距离。 之间的距离就是直线与抛物线的最短距离。
抛物线与圆的位置关系
只限于抛物线与圆有共同对称轴的情况,研究抛物线与圆的最短距离。
由于圆的半径是不变的,抛物线与圆的最短距离就转化为定圆的圆心
与抛物线的最短距离。
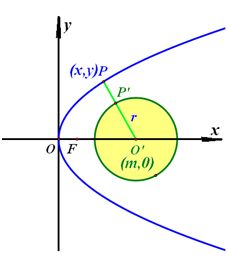
如图,设抛物线 : :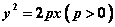 上点 上点 ,圆 ,圆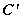 : :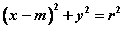 , , 与圆 与圆 交于点 交于点 ,则 ,则

求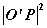 的最小值转化为求二次函数 的最小值转化为求二次函数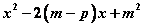
在区间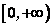 上的最小值,于是 上的最小值,于是
 。 。
12.3.4抛物线的焦点弦的性质<-->12.4.1直线与圆锥曲线的位置关系
全网搜索"12.3.5关于抛物线的几个重要结论"相关
|

