|
7.1.6三角形形状的判定<-->返回列表
正弦定理和余弦定理在实际测量中的应用举例
有关名词、术语
- 仰角和俯角:与目标在同一铅垂平面内的水平线和目标视线的夹角。目标视线在水平线上面时角仰角,目标视线在视平线下方时叫做俯角。如图示:
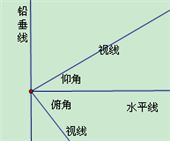 - 方位角:一般是指正北方向顺时针转到目标线的水平角,如果方位角是45°,指北偏东45°,即东北方向。
- 坡角:坡面与水平面的夹角。
- 坡度:坡面的铅直高度与水平宽度之比。
- 基线:在测量上,根据测量需要适当确定的线段叫做基线。
详解:
测量一定要选用基线,因为无论应用正弦定理还是余弦定理解三角形时,至少应已知一边的长度;
一般来说,基线越长,测量的精确度越高。
解三角形应用题的一般思路
解三角形应用题的一般思路如下:
1 读懂题意、理解问题的实际背景,明确已知和所求,准确理解应用题中的有关术语、名称,如仰角、俯角、方位角等,理清量与量之间的关系;
2 根据题意画出示意图,将实际问题抽象成解三角形模型;
3 合理选择正弦定理和余弦定理求解;
4 将三角形的解还原为实际问题,注意实际问题中的单位、结果要求近似等。
|

