|
7.1.2三角形中正弦定理的应用<-->7.1.4三角形中余弦定理的应用
余弦定理
余弦定理:在一个三角形中,任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍所得的差。
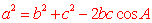 ; ;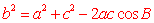 ; ;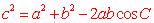
应用余弦定理,我们就可以从已知的两边和夹角计算出三角形的的第三条边
也可以变形写成:
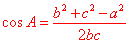 ; ;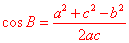 ; ;
从上面可知,余弦定理及其推论把用“边、角、边”和“边、边、边”判定三角形全等的方法从数量化的角度进行了刻画,使其变成了可以计算的公式。
理解、应用余弦定理应注意以下四点:
1 余弦定理揭示了任意三角形边角之间的客观规律,是解三角形的重要工具;
2 余弦定理是勾股定理的推广,勾股定理是余弦定理的特例;
3 在余弦定理中,每一个等式均含有四个量,利用方程的观点,可以知三求一;
4 运用余弦定理时,因为已知三边求角,或已知两边及夹角求另一边,由三角形全等的判定定理知,三角形是确定的,所以解也是唯一的。
7.1.2三角形中正弦定理的应用<-->7.1.4三角形中余弦定理的应用
全网搜索"7.1.3余弦定理"相关
|

