|
返回列表<-->5.1.2弧度制
任意角的概念
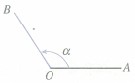
〖概念〗角可以看作是平面内一条射线绕着端点从一个位置旋转到另一个位置所形成的图形，设一条射线的端点是O，它从起始位置OA按逆时针方向旋转到终止位置OB，则形成了一个角α，点O是角的顶点，射线OA、OB分别是角α的始边和终边。
〖分类〗
1、正角：按逆时针方向旋转形成的角叫做正角；
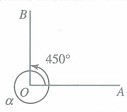
如图，∠α=450°.
2、负角：按顺时针方向旋转形成的角叫做负角；
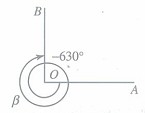
如图，∠α=－630°.
3、零角：如果一条射线没有任何旋转，我们称它形成了一个零角。
〖代数表示〗为了简便起见，在不引起混淆的前提下，“角α”或“∠α”可以简记作“α”。如果α是零角，那么α=0°.
〖几何表示〗如图所示
详解：
〖概念总结〗角度正负的记忆：逆正，顺负，不动零。
〖概念辨析〗
1、要正确理解正角、负角、零角的概念，既要注意旋转量，也要注意旋转方向。
2、表示角时，应注意箭头的方向不可丢掉，因为箭头的方向代表角的正负。
〖相关知识〗
终边相同的角，象限角，坐标轴上的角，任意角与实数集。
终边相同的角
〖定义〗所有与角α终边相同的角，连同角α在内，可构成一个集合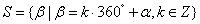 ，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和。
〖几何表示〗如图所示
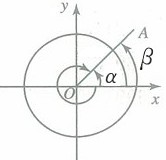
详解：
〖概念辨析〗
（1）相等的角，终边一定相同，终边相同的角不一定相等。
（2）k是整数，α是任意角，终边相同的角有无数多个，它们相差360°的整数倍。
〖相关知识〗
任意角的概念，象限角，坐标轴上的角，任意角与实数集。
象限角
〖定义〗把角放在直角坐标系中，使角的顶点与坐标原点重合，角的始边放在x轴的正半轴上，角的终边落在第几象限就将该角叫做第几象限角。如果角的终边落在坐标轴上，就认为这个角不属于任何一个象限。
〖代数表示〗
终边在第一象限的角的集合: {β｜n·360°<β<n·360°+90°，n∈Z}
终边在第二象限的角的集合: {β｜n·360°+90°<β<n·360°+180°，n∈Z}
终边在第三象限的角的集合: {β｜n·360°+180°<β<n·360°+270°，n∈Z}
终边在第四象限的角的集合: {β｜n·360°+270°<β<n·360°+360°，n∈Z}
〖几何表示〗
详解：
〖记忆方法〗记忆方法、口诀
〖概念辨析〗如果角的顶点不与坐标原点重合，或者角的始边不与x轴非负半轴重合，则不能判断角在哪一象限，也就是说它不能称作象限角。
〖相关知识〗
坐标轴上的角
坐标轴上的角
〖定义〗在直角坐标系内，角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，那么角的终边落在坐标轴上，我们就说这个角是坐标轴上的角。
〖代数表示〗符号或字母表示
与x轴正半轴终边相同的角的集合为 {β｜β=k•360°，k∈Z}
与x轴负半轴终边相同的角的集合为 {β｜β=180º+k•360°，k∈Z}
与y轴正半轴终边相同的角的集合为 {β｜β=90°+k•360°，k∈Z}
与y轴负半轴终边相同的角的集合为 {β｜β=270°+k•360°，k∈Z}
终边在x轴上的角的集合为 {β｜β=n•180°，n∈Z}
终边在y轴上的角的集合为{β｜β=90°+n•180°，n∈Z}
终边在坐标轴上的角的集合为 {β｜β=n•90°，n∈Z}
〖几何表示〗
|
