|
2.1.1命题<-->2.1.3四种命题的相互关系
命题的四种形式
①命题四种形式的定义:
Ⅰ、原命题与逆命题:
在两个命题中,如果第一个命题的条件(或题设)是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题;如果把其中一个命题叫做原命题,那么另一个叫做原命题的逆命题。
Ⅱ、原命题与否命题:
在两个命题中,一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定,这样的两个命题就叫做互否命题,若把其中一个命题叫做原命题,则另一个就叫做原命题的否命题。
Ⅲ、原命题与逆否命题:
在两个命题中,一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定,这样的两个命题就叫做互为逆否命题,若把其中一个命题叫做原命题,则另一个就叫做原命题的逆否命题。
②四种命题的形式表述:
原命题:若$p$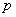 ,则$q$ ,则$q$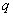 ; ;
逆命题:若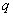 ,则 ,则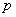 (交换原命题的条件和结论); (交换原命题的条件和结论);
否命题:若非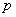 ,则非 ,则非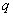 (同时否定原命题的条件和结论); (同时否定原命题的条件和结论);
逆否命题:若非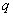 ,则非 ,则非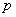 (交换原命题的条件和结论,并同时否定)。 (交换原命题的条件和结论,并同时否定)。
③命题的四种形式的内在联系:
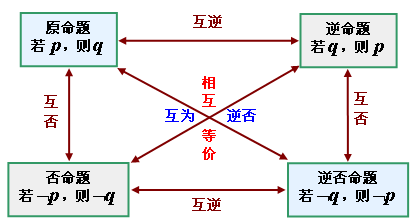
④四种命题的真假关系:
Ⅰ、原命题与逆否命题是互为逆否命题,逆命题和否命题也是互为逆否命题;
Ⅱ、两个命题互为逆否命题,它们有相同的真假性;
Ⅲ、两个命题为互逆命题或互否命题,它们的真假性没有关系。
Ⅳ、由于原命题和它的逆否命题具有相同的真假性,所以在直接证明某一个命题为真命题有困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题。这就是“反证法”的依据。
实例:
写出下列命题的逆命题、否命题和逆否命题
命题:矩形的两条对角线互相平分
解:原命题:若四边形是矩形,则它的两条对角线互相平分;
逆命题:若四边形的两条对角线互相平分,则它是矩形;
否命题:若四边形不是矩形,则它的两条对角线不互相平分;
逆否命题:若四边形的两条对角线不互相平分,则它不是矩形。
2.1.1命题<-->2.1.3四种命题的相互关系
全网搜索"2.1.2四种命题"相关
|

