|
3.3.2 二次函数的性质<-->3.3.4 一元二次方程与二次函数的关系
二次函数闭区间上最值
设二次函数$y=ax^2+bx+c(a \neq 0)$定义在闭区间$[\alpha,\beta]$上,对称轴为$x=-\dfrac{b}{2a}$,其最值情况如下:
Ⅰ、若a>0,则y的最大值以对称轴为$x=-\dfrac{b}{2a}$ 相对于闭区间$[\alpha,\beta]$中点$\dfrac{\alpha+\beta}{2}$为界,“两类分”;y的最小值以对称轴为 $x=-\dfrac{b}{2a}$相对于闭区间$[\alpha,\beta]$的端点为界,“三类分”。即
$y_{max}=\begin{cases}f({\beta}),&-\dfrac{b}{2a} \leqslant \dfrac{\alpha+\beta}{2} \\ f({\alpha}),&-\dfrac{b}{2a} \geqslant \dfrac{\alpha+\beta}{2} \end{cases}$
$y_{min}=\begin{cases}f({\alpha}),&-\dfrac{b}{2a} < \alpha \\ f\left(-\dfrac{b}{2a}\right),& \alpha \leqslant -\dfrac{b}{2a} \leqslant \beta \\ f({\beta}),&-\dfrac{b}{2a} > \beta\end{cases}$
简而言之,
若 ,则 ,则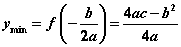 , ,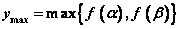 ; ;
若 ,则 ,则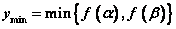 , ,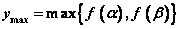 。 。
Ⅱ、若 a<0,则y的最大值以对称轴为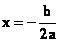 相对于闭区间 相对于闭区间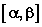 的端点为界,“三类分”;y的最小值以对称轴为 的端点为界,“三类分”;y的最小值以对称轴为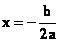 相对于闭区间 相对于闭区间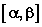 的中点 的中点 为界,“两类分”。即 为界,“两类分”。即
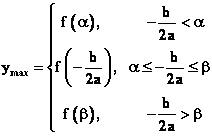 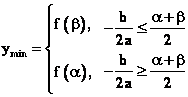 , ,
简而言之,
若 ,则 ,则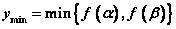 , ,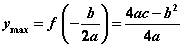 ; ;
若 ,则 ,则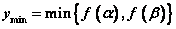 , ,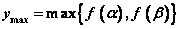 。 。
3.3.2 二次函数的性质<-->3.3.4 一元二次方程与二次函数的关系
全网搜索"3.3.3 二次函数在闭区间上的最值"相关
|

