|
2023年高考数学新高考Ⅱ-13<-->2023年高考数学新高考Ⅱ-15
(5分)底面边长为4的正四棱锥被平行于其底面的平面所截,截去一个底面边长为2,高为3的正四棱锥,所得棱台的体积为 ____.
分析:根据题意易知△$SO_{1}A_{1}\backsim \Delta SOA$,从而可求出台体的高,再根据台体的体积公式,计算即可得解.
解:如图所示,根据题意易知△$SO_{1}A_{1}\backsim \Delta SOA$,
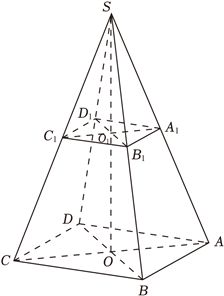
$\therefore$$\dfrac{S{O}_{1}}{SO}=\dfrac{{O}_{1}{A}_{1}}{OA}=\dfrac{\sqrt{2}}{2\sqrt{2}}=\dfrac{1}{2}$,又$SO_{1}=3$,
$\therefore SO=6$,$\therefore OO_{1}=3$,又上下底面正方形边长分别为2,4,
$\therefore$所得棱台的体积为$\dfrac{1}{3}\times (4+16+\sqrt{4\times 16})\times 3=28$.
故答案为:28.
点评:本题考查台体的体积的求解,化归转化思想,方程思想,属基础题.
2023年高考数学新高考Ⅱ-13<-->2023年高考数学新高考Ⅱ-15
全网搜索"2023年高考数学新高考Ⅱ-14"相关
|

