2023年天津

Processing math: 100%

活在当下，做最好的自己！

收藏夹
我的

当前：首页 > 数学 > 高考题 > 2023 > 2023年天津

2023年高考数学天津1（5分）已知集合

$U=\{1$ ，2，3，4，

$5\}$ ，

$A=\{1$ ，

$3\}$ ，

$B=\{1$ ，2，

$4\}$ ，则

$\complement _{U}B\bigcup A=($ 　　

$)$
A．

$\{1$ ，3，

$5\}$ B．

$\{1$ ，

$3\}$ C．

$\{1$ ，2，

$4\}$ D．

$\{1$ ，2，4，

$5\}$ 【答案详解】

2023年高考数学天津2（5分）“

$a^{2}=b^{2}$ ”是“

$a^{2}+b^{2}=2ab$ ”的

$($ 　　

$)$
A．充分不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件【答案详解】

2023年高考数学天津3（5分）若

$a=1.01^{0.5}$ ，

$b=1.01^{0.6}$ ，

$c=0.6^{0.5}$ ，则

$($ 　　

$)$
A．

$c > a > b$ B．

$c > b > a$ C．

$a > b > c$ D．

$b > a > c$ 【答案详解】

2023年高考数学天津4（5分）函数

$f(x)$ 的图象如图所示，则

$f(x)$ 的解析式可能为

$($ 　　

$)$

A．

$\dfrac{5({{e^x}-{e^{-x}}})}{{x^2}+2}$ B．

$\dfrac{5\sin x}{{x^2}+1}$
C．

$\dfrac{5({{e^x}+{e^{-x}}})}{{x^2}+2}$ D．

$\dfrac{5\cos x}{{x^2}+1}$ 【答案详解】

2023年高考数学天津5（5分）已知函数

$f(x)$ 的一条对称轴为直线

$x=2$ ，一个周期为4，则

$f(x)$ 的解析式可能为

$($ 　　

$)$
A．

$\sin (\dfrac{\pi }{2}x)$ B．

$\cos (\dfrac{\pi }{2}x)$ C．

$\sin (\dfrac{\pi }{4}x)$ D．

$\cos (\dfrac{\pi }{4}x)$ 【答案详解】

2023年高考数学天津6（5分）已知

$\{a_{n}\}$ 为等比数列，

$S_{n}$ 为数列

$\{a_{n}\}$ 的前

$n$ 项和，

$a_{n+1}=2S_{n}+2$ ，则

$a_{4}$ 的值为

$($ 　　

$)$
A．3 B．18 C．54 D．152【答案详解】

2023年高考数学天津7（5分）调查某种花萼长度和花瓣长度，所得数据如图所示，其中相关系数

$r=0.8245$ ，下列说法正确的是

$($ 　　

$)$

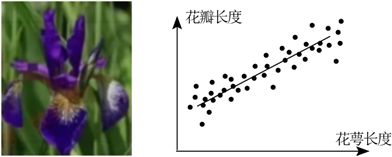
A．花瓣长度和花萼长度没有相关性
B．花瓣长度和花萼长度呈现负相关
C．花瓣长度和花萼长度呈现正相关
D．若从样本中抽取一部分，则这部分的相关系数一定是0.8245【答案详解】

2023年高考数学天津8（5分）在三棱锥

$P-ABC$ 中，线段

$PC$ 上的点

$M$ 满足

$PM=\dfrac{1}{3}PC$ ，线段

$PB$ 上的点

$N$ 满足

$PN=\dfrac{2}{3}PB$ ，则三棱锥

$P-AMN$ 和三棱锥

$P-ABC$ 的体积之比为

$($ 　　

$)$
A．

$\dfrac{1}{9}$ B．

$\dfrac{2}{9}$ C．

$\dfrac{1}{3}$ D．

$\dfrac{4}{9}$ 【答案详解】

2023年高考数学天津9（5分）双曲线

$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a > 0,b > 0)$ 的左、右焦点分别为

$F_{1}$ ，

$F_{2}$ ．过

$F_{2}$ 作其中一条渐近线的垂线，垂足为

$P$ ．已知

$\vert PF_{2}\vert =2$ ，直线

$PF_{1}$ 的斜率为

$\dfrac{\sqrt{2}}{4}$ ，则双曲线的方程为

$($ 　　

$)$
A．

$\dfrac{x^2}{8}-\dfrac{y^2}{4}=1$ B．

$\dfrac{x^2}{4}-\dfrac{y^2}{8}=1$ C．

$\dfrac{x^2}{4}-\dfrac{y^2}{2}=1$ D．

$\dfrac{x^2}{2}-\dfrac{y^2}{4}=1$ 【答案详解】

2023年高考数学天津10（5分）已知

$i$ 是虚数单位，化简

$\dfrac{5+14i}{2+3i}$ 的结果为____．
【答案详解】

2023年高考数学天津11（5分）在

$(2x^{3}-\dfrac{1}{x})^{6}$ 的展开式中，

$x^{2}$ 项的系数为____．
【答案详解】

2023年高考数学天津12（5分）过原点的一条直线与圆

$C:(x+2)^{2}+y^{2}=3$ 相切，交曲线

$y^{2}=2px(p > 0)$ 于点

$P$ ，若

$\vert OP\vert =8$ ，则

$p$ 的值为 ____．
【答案详解】

2023年高考数学天津13（5分）甲、乙、丙三个盒子中装有一定数量的黑球和白球，其总数之比为

$5:4:6$ ．这三个盒子中黑球占总数的比例分别为

$40%$ ，

$25%$ ，

$50%$ ．现从三个盒子中各取一个球，取到的三个球都是黑球的概率为____；将三个盒子混合后任取一个球，是白球的概率为____．
【答案详解】

2023年高考数学天津14（5分）在

$\Delta ABC$ 中，

$\angle A=60^\circ$ ，

$\vert \overrightarrow{BC}\vert =1$ ，点

$D$ 为

$AB$ 的中点，点

$E$ 为

$CD$ 的中点，若设

$\overrightarrow{AB}=\overrightarrow{a}$ ，

$\overrightarrow{AC}=\overrightarrow{b}$ ，则

$\overrightarrow{AE}$ 可用

$\overrightarrow{a}$ ，

$\overrightarrow{b}$ 表示为____；若

$\overrightarrow{BF}=\dfrac{1}{3}\overrightarrow{BC}$ ，则

$\overrightarrow{AE}\cdot \overrightarrow{AF}$ 的最大值为 ____．【答案详解】

2023年高考数学天津15（5分）若函数

$f(x)=ax^{2}-2x-\vert x^{2}-ax+1\vert$ 有且仅有两个零点，则

$a$ 的取值范围为____．
【答案详解】

2023年高考数学天津16（14分）在

$\Delta ABC$ 中，角

$A$ ，

$B$ ，

$C$ 的对边分别为

$a$ ，

$b$ ，

$c$ ．已知

$a=\sqrt{39}$ ，

$b=2$ ，

$\angle A=120^\circ$ ．
（Ⅰ）求

$\sin B$ 的值；
（Ⅱ）求

$c$ 的值；
（Ⅲ）求

$\sin (B-C)$ 的值．【答案详解】

2023年高考数学天津17（15分）在三棱台

$ABC-A_{1}B_{1}C_{1}$ 中，若

$A_{1}A\bot$ 平面

$ABC$ ，

$AB\bot AC$ ，

$AB=AC=AA_{1}=2$ ，

$A_{1}C_{1}=1$ ，

$M$ ，

$N$ 分别为

$BC$ ，

$AB$ 中点．
（Ⅰ）求证：

$A_{1}N//$ 平面

$C_{1}MA$ ；
（Ⅱ）求平面

$C_{1}MA$ 与平面

$ACC_{1}A_{1}$ 所成角的余弦值；
（Ⅲ）求点

$C$ 到平面

$C_{1}MA$ 的距离．

【答案详解】

2023年高考数学天津18（15分）设椭圆

$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$ 的左、右顶点分别为

$A_{1}$ ，

$A_{2}$ ，右焦点为

$F$ ，已知

$\vert A_{1}F\vert =3$ ，

$\vert A_{2}F\vert =1$ ．
（Ⅰ）求椭圆方程及其离心率；
（Ⅱ）已知点

$P$ 是椭圆上一动点（不与顶点重合），直线

$A_{2}P$ 交

$y$ 轴于点

$Q$ ，若△

$A_{1}PQ$ 的面积是△

$A_{2}FP$ 面积的二倍，求直线

$A_{2}P$ 的方程．【答案详解】

2023年高考数学天津19（15分）已知

$\{a_{n}\}$ 是等差数列，

$a_{2}+a_{5}=16$ ，

$a_{5}-a_{3}=4$ ．
（Ⅰ）求

$\{a_{n}\}$ 的通项公式和

$\sum\limits_{i={2^{n-1}}}^{{2^n}-1}{a_i}$ ；
（Ⅱ）已知

$\{b_{n}\}$ 为等比数列，对于任意

$k\in N^{*}$ ，若

$2^{k-1}\leqslant n\leqslant 2^{k}-1$ ，则

$b_{k} < a_{n} < b_{k+1}$ ．

$(i)$ 当

$k\geqslant 2$ 时，求证：

$2^{k}-1 < b_{n} < 2^{k}+1$ ；

$(ii)$ 求

$\{b_{n}\}$ 的通项公式及其前

$n$ 项和．【答案详解】

2023年高考数学天津20（16分）已知函数

$f(x)=(\dfrac{1}{x}+\dfrac{1}{2})\ln (x+1)$ ．
（Ⅰ）求曲线

$y=f(x)$ 在

$x=2$ 处的切线斜率；
（Ⅱ）当

$x > 0$ 时，求证：

$f(x) > 1$ ；
（Ⅲ）证明：

$\dfrac{5}{6} < \ln (n!)-(n+\dfrac{1}{2})\ln n+n\leqslant 1$ ．【答案详解】

开心教练从2004年开始自费开设这个网站. 为了可以持续免费提供这些内容, 并且没有广告干扰，请大家随意打赏，谢谢！,
（微信中可直接长按微信打赏二维码。）

微信	支付宝