|
2023年高考数学北京14<-->2023年高考数学北京16
(5分)设$a > 0$,函数$f(x)=\left\{{\left.\begin{array}{l}{x+2,x < -a,}\\ {\sqrt{{a^2}-{x^2}},-a\leqslant x\leqslant a,}\\ {-\sqrt{x}-1,x > a\cdot }\end{array}\right.}\right.$给出下列四个结论,正确的序号为____.
①$f(x)$在区间$(a-1,+\infty )$上单调递减;
②当$a\geqslant 1$时,$f(x)$存在最大值;
③设$M(x_{1}$,$f(x_{1}))(x_{1}\leqslant a)$,$N(x_{2}$,$f(x_{2}))(x_{2} > a)$,则$\vert MN\vert > 1$;
④设$P(x_{3}$,$f(x_{3}))(x_{3} < -a)$,$Q(x_{4}$,$f(x_{4}))(x_{4}\geqslant -a)$,若$\vert PQ\vert$存在最小值,则$a$的取值范围时$(0$,$\dfrac{1}{2}]$.
答案:②③
分析:先大致画出$f(x)$的草图,再根据四个选项逐一判断,对于选项①,取特殊值$a=2$判断函数函调性即可;对于选项②,分别判断$a\geqslant 1$时每段函数的最值情况,再判断是否存在最大值;对于选项③,结合图象分析$\vert MN\vert$最小值的情况,即可得出$\vert MN\vert$的范围;对于选项④,针对图像分析$\vert PQ\vert$存在最小值的情况,可得直线$y=-x$需要与前两段函数图像都有交点才可满足,进而可求出$a$的取值范围.
解:$a > 0$,当$x < -a$时,$f(x)=x+2$,图像为一次函数;
当$-a\leqslant x\leqslant a$时,$f(x)=\sqrt{{a}^{2}{-x}^{2}}$,图像为以$(0,0)$为圆心,$a$为半径的圆的上半弧;
当$x > a$时,$f(x)=-\sqrt{x}-1$,图像为单调递减的曲线;
其函数图象大致如下:

选项①,取$a=2$,$f(x)$在区间$(-1,+\infty )$上先单调递增,后单调递减,选项①错误;
选项②,当$a\geqslant 1$时,
$x < -a$,$f(x)=x+2 < 2-a < 2-1=1$;
$-a\leqslant x\leqslant a$,$f(x)=\sqrt{{a}^{2}{-x}^{2}}$,最大值为$a\geqslant 1$;
$x > a$,$f(x)=-\sqrt{x}-1 < -\sqrt{a}-1 < -2$;
所以$f(x)$存在最大值$a$,选项②正确;
选项③,由图可知,当点$M$位于点$B$,点$N$无限接近于点$D$时,$MN$的长度最短,
当$N$无限接近于点$D$时,$x_{D}$无限接近于$x=a$,
所以$\vert MN\vert > y_{M}-y_{N}=1+\sqrt{a} > 1$,选项③正确;
选项④,如上图,若$\vert PQ\vert$存在最小值,则$P$、$Q$应该是直线$y=-x$分别于$f(x)=x+2$,$f(x)=\sqrt{{a}^{2}{-x}^{2}}$的交点,
直线$y=-x$与$f(x)=\sqrt{{a}^{2}{-x}^{2}}$一定存在交点,而直线$y=-x$与$f(x)=x+2$不一定存在交点,
当直线$y=-x$与$f(x)=x+2$没有交点时,$-a\leqslant -1$,即$a\geqslant 1$,此时由于$P$点取不到,$\vert PQ\vert$不存在最小值,
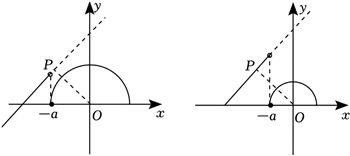
所以$0 < a < 1$,选项④错误.
故答案为:②③.
点评:本题考查分段函数的应用问题,考查学生用数形结合方法分析试题的能力,属于难题.
2023年高考数学北京14<-->2023年高考数学北京16
全网搜索"2023年高考数学北京15"相关
|

