|
2023年高考数学北京8<-->2023年高考数学北京10
(4分)刍曹是我国传统建筑造型之一,蕴含着丰富的数学元素.安装灯带可以勾勒出建筑轮廓,展现造型之美.如图,某屋顶可视为五面体$ABCDEF$,四边形$ABFE$和$CDEF$是全等的等腰梯形,$\Delta ADE$和$\Delta BCF$是全等的等腰三角形.若$AB=25m$,$BC=AD=10m$,且等腰梯形所在的面、等腰三角形所在的面与底面夹角的正切值均为$\dfrac{\sqrt{14}}{5}$.为这个模型的轮廓安装灯带(不计损耗),则所需灯带的长度为$($ $)$

A.$102m$ B.$112m$ C.$117m$ D.$125m$
答案:$C$
分析:根据题意及对称性可知底面四边形$ABCD$为矩形,再根据三垂线定理作出等腰梯形所在的面、等腰三角形所在的面与底面夹角,再题目中的数据,计算即可求解.
解:根据题意及对称性可知底面四边形$ABCD$为矩形,
设$E$,$F$在底面矩形的射影点分别为$M$,$N$,
设$AD$与$BC$的中点分别为$P$,$Q$,则$M$,$N$在线段$PQ$上,如图,
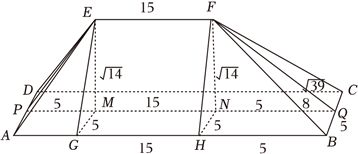
过$M$,$N$分别作$AB$的垂线,垂足点分别为$G$,$H$,连接$HF$,$FQ$,
则根据题意及三垂线定理易得$\tan \angle EPM=\tan \angle EGM=\tan \angle FHN=\tan \angle FQN=\dfrac{\sqrt{14}}{5}$,
又$MG=NH=5$,$\therefore FM=FN=\sqrt{14}$,$\therefore PM=QN=5$,$\therefore EP=FQ=\sqrt{14+25}=\sqrt{39}$,
$\therefore MN=PQ-PM-QN=AB-PM-QN=25-5-5=15$,$\therefore EF=MN=15$,
又易知$BC\bot QN$,$FN\bot$底面矩形$ABCD$,
$\therefore$根据三垂线定理可知$BC\bot FQ$,又$BQ=5$,$FQ=\sqrt{39}$,
$\therefore FB=\sqrt{39+25}=8$,$\therefore ED=EA=FC=FB=8$,
$\therefore$该多面体的所有棱长和为$8\times 4+(25+10)\times 2+15=117$.
故所需灯带的长度为$117m$.
故选:$C$.
点评:本题考查几何体的所有棱长和的求解,三垂线定理作二面角,化归转化思想,属中档题.
2023年高考数学北京8<-->2023年高考数学北京10
全网搜索"2023年高考数学北京9"相关
|

