|
2023年高考数学北京5<-->2023年高考数学北京7
(4分)已知抛物线$C:y^{2}=8x$的焦点为$F$,点$M$在$C$上,若$M$到直线$x=-3$的距离为5,则$\vert MF\vert =($ $)$
A.7 B.6 C.5 D.4
答案:$D$
分析:本题只需将点$M$到$x=-3$的距离,转化为到准线$x=-2$的距离,再根据抛物线定义即可求得.
解:如图所示,因为点$M$到直线$x=-3$的距离$\vert MR\vert =5$,
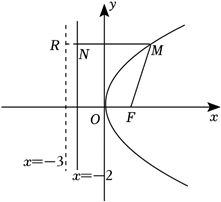
$\therefore$点$M$到直线$x=-2$的距离$\vert MN\vert =4$.
由方程$y^{2}=8x$可知,$x=-2$是抛物线的准线,
又抛物线上点$M$到准线$x=-2$的距离和到焦点$F$的距离相等,
故$\vert MF\vert =\vert MN\vert =4$.
故选:$D$.
点评:本题考查了抛物线定义的应用,属简单题.
2023年高考数学北京5<-->2023年高考数学北京7
全网搜索"2023年高考数学北京6"相关
|

