|
2021年高考数学上海8<-->2021年高考数学上海10
9.(5分)已知圆柱的底面圆半径为1,高为2,$AB$为上底面圆的一条直径,$C$是下底面圆周上的一个动点,则$ABC$的面积的取值范围为 ____.
分析:上顶面圆心记为$O$,下底面圆心记为$O'$,连结$OC$,过点$C$作$CM\bot AB$,垂足为点$M$,由于$AB$为定值,则$S_{\Delta ABC}$的大小随着$CM$的长短变化而变化,
分别求解$CM$的最大值和最小值,即可得到答案.
解:如图1,上底面圆心记为$O$,下底面圆心记为$O'$,
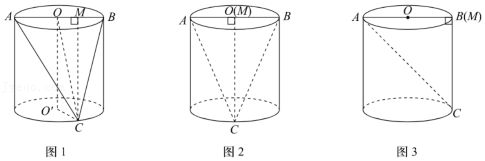
连结$OC$,过点$C$作$CM\bot AB$,垂足为点$M$,
则${S}_{\Delta ABC}=\dfrac{1}{2}\times AB\times CM$,
根据题意,$AB$为定值2,所以$S_{\Delta ABC}$的大小随着$CM$的长短变化而变化,
如图2所示,当点$M$与点$O$重合时,$CM=OC=\sqrt{{1}^{2}+{2}^{2}}=\sqrt{5}$,
此时$S_{\Delta ABC}$取得最大值为$\dfrac{1}{2}\times 2\times \sqrt{5}=\sqrt{5}$;
如图3所示,当点$M$与点$B$重合,$CM$取最小值2,
此时$S_{\Delta ABC}$取得最小值为$\dfrac{1}{2}\times 2\times 2=2$.
综上所述,$S_{\Delta ABC}$的取值范围为$[2,\sqrt{5}]$.
故答案为:$[2,\sqrt{5}]$.
点评:本题考查了空间中的最值问题,将三角形面积的最值问题转化为求解线段$CM$的最值问题进行求解是解题的关键,考查了空间想象能力与逻辑推理能力,属于中档题.
2021年高考数学上海8<-->2021年高考数学上海10
全网搜索"2021年高考数学上海9"相关
|

