|
2020年高考数学新高考Ⅱ-18<-->2020年高考数学新高考Ⅱ-20
(12分)为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的$PM2.5$和$SO_{2}$浓度(单位:$\mu g/m^{3})$,得下表:
 |
$[0$,$50]$ |
$(50$,$150]$ |
$(150$,$475]$ |
| $[0$,$35]$ |
32 |
18 |
4 |
| $(35$,$75]$ |
6 |
8 |
12 |
| $(75$,$115]$ |
3 |
7 |
10 |
(1)估计事件“该市一天空气中$PM2.5$浓度不超过75,且$SO_{2}$浓度不超过150”的概率;
(2)根据所给数据,完成下面的$2\times 2$列联表:
 |
$[0$,$150]$ |
$(150$,$475]$ |
| $[0$,$75]$ |
|
|
| $(75$,$115]$ |
|
|
(3)根据(2)中的列联表,判断是否有$99%$的把握认为该市一天空气中$PM2.5$浓度与$SO_{2}$浓度有关?
附:$K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| $P(K^{2}\geqslant k)$ |
0.050 |
0.010 |
0.001 |
| $k$ |
3.841 |
6.635 |
10.828 |
分析:(1)用频率估计概率,从而得到“该市一天空气中$PM2.5$浓度不超过75,且$SO_{2}$浓度不超过150”的概率;
(2)根据题目所给的数据填写$2\times 2$列联表即可;
(3)计算$K^{2}$,对照题目中的表格,得出统计结论.
解答:解:(1)用频率估计概率,从而得到“该市一天空气中$PM2.5$浓度不超过75,且$SO_{2}$浓度不超过150”的概率$P=\dfrac{32+18+6+8}{100}=0.64$;
(2)根据所给数据,可得下面的$2\times 2$列联表:
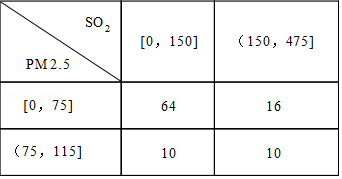
(3)根据(2)中的列联表,
由${K^2}=\dfrac{n{{(ad-bc)}^2}}{(a+b)(c+d)(a+c)(b+d)}=\dfrac{100\times (64\times 10-16\times 10)^{2}}{80\times 20\times 74\times 26}\approx 7.484>6.635$,
$P(K^{2}\geqslant 6.635)=0.01$;
故有$99%$的把握认为该市一天空气中$PM2.5$浓度与$SO_{2}$浓度有关,
点评:本题考查了独立性检验的应用,用频率估计概率,属于基础题.
2020年高考数学新高考Ⅱ-18<-->2020年高考数学新高考Ⅱ-20
全网搜索"2020年高考数学新高考Ⅱ-19"相关
|

