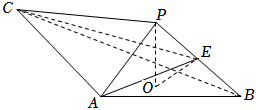
2022年高考数学新高考Ⅱ-20(12分)如图,$PO$是三棱锥$P-ABC$的高,$PA=PB$,$AB\bot AC$,$E$为$PB$的中点.
(1)证明:$OE//$平面$PAC$;
(2)若$\angle ABO=\angle CBO=30^\circ$,$PO=3$,$PA=5$,求二面角$C-AE-B$的正弦值.
 【答案详解】 【答案详解】 |
| 2019年高考数学天津--理17(2019天津卷计算题)(本小题满分13分)如图,平面,,,,,。(Ⅰ)求证:平面;(Ⅱ)求直线与平面所成角的正弦值;(Ⅲ)若二面角的余弦值为,求线段的长。【出处】2019年普通高等学校招生全国统一考试(天津卷):理数第17题【答案】建立以为原点,分别以,,的方【答案详解】 |
| 2019年高考数学北京--理16(2019北京卷计算题)(本小题分)如图,在四棱锥中,平面,,,,。为的中点,点在上,且。(Ⅰ)求证:平面;(Ⅱ)求二面角的余弦值;(Ⅲ)设点在上,且。判断直线是否在平面内,说明理由。【出处】2019年普通高等学校招生全国统一考试(北京卷):理数第16题【答案【答案详解】 |

