|
2022年高考数学新高考Ⅱ-19<-->2022年高考数学新高考Ⅱ-21
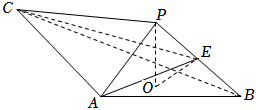
(12分)如图,$PO$是三棱锥$P-ABC$的高,$PA=PB$,$AB\bot AC$,$E$为$PB$的中点.
(1)证明:$OE//$平面$PAC$;
(2)若$\angle ABO=\angle CBO=30^\circ$,$PO=3$,$PA=5$,求二面角$C-AE-B$的正弦值.
分析:(1)连接$OA$,$OB$,可证得$OA=OB$,延长$BO$交$AC$于点$F$,可证得$OE//PF$,由此得证;
(2)建立空间直角坐标系,写出各点的坐标,再求出平面$ACE$及平面$ABE$的法向量,利用向量的夹角公式得解.
解:(1)证明:连接$OA$,$OB$,依题意,$OP\bot$平面$ABC$,
又$OA\subset$平面$ABC$,$OB\subset$平面$ABC$,则$OP\bot OA$,$OP\bot OB$,
$\therefore \angle POA=\angle POB=90^\circ$,
又$PA=PB$,$OP=OP$,则$\Delta POA\cong \Delta POB$,
$\therefore OA=OB$,
延长$BO$交$AC$于点$F$,又$AB\bot AC$,则在$\rm{Rt}\Delta ABF$中,$O$为$BF$中点,连接$PF$,
在$\Delta PBF$中,$O$,$E$分别为$BF$,$BP$的中点,则$OE//PF$,
$\because OE\not\subset$平面$PAC$,$PF\subset$平面$PAC$,
$\therefore OE//$平面$PAC$;
(2)过点$A$作$AM//OP$,以$AB$,$AC$,$AM$分别为$x$轴,$y$轴,$z$轴建立如图所示的空间直角坐标系,

由于$PO=3$,$PA=5$,由(1)知$OA=OB=4$,
又$\angle ABO=\angle CBO=30^\circ$,则$AB=4\sqrt{3}$,
$\therefore$$P(2\sqrt{3},2,3),B(4\sqrt{3},0,0),A(0,0,0),E(3\sqrt{3},1,\dfrac{3}{2})$,
又$AC=AB\tan 60^\circ =12$,即$C(0$,12,$0)$,
设平面$AEB$的一个法向量为$\overrightarrow{n}=(x,y,z)$,又$\overrightarrow{AB}=(4\sqrt{3},0,0),\overrightarrow{AE}=(3\sqrt{3},1,\dfrac{3}{2})$,
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{AB}=4\sqrt{3}x=0}\\ {\overrightarrow{n}\cdot \overrightarrow{AE}=3\sqrt{3}x+y+\dfrac{3}{2}z=0}\end{array}\right.$,则可取$\overrightarrow{n}=(0,3,-2)$,
设平面$AEC$的一个法向量为$\overrightarrow{m}=(a,b,c)$,又$\overrightarrow{AC}=(0,12,0),\overrightarrow{AE}=(3\sqrt{3},1,\dfrac{3}{2})$,
则$\left\{\begin{array}{l}{\overrightarrow{m}\cdot \overrightarrow{AC}=12b=0}\\ {\overrightarrow{m}\cdot \overrightarrow{AE}=3\sqrt{3}a+b+\dfrac{3}{2}c=0}\end{array}\right.$,则可取$\overrightarrow{m}=(-\sqrt{3},0,6)$,
设锐二面角$C-AE-B$的平面角为$\theta$,则$\cos \theta =\vert \cos < \overrightarrow{m},\overrightarrow{n} > \vert =\vert \dfrac{\overrightarrow{m}\cdot \overrightarrow{n}}{\vert \overrightarrow{m}\vert \vert \overrightarrow{n}\vert }\vert =\dfrac{4\sqrt{3}}{13}$,
$\therefore$$\sin \theta =\sqrt{1-co{s}^{2}\theta }=\dfrac{11}{13}$,即二面角$C-AE-B$正弦值为$\dfrac{11}{13}$.
点评:本题考查线面平行的判定以及利用空间向量求解二面角的正弦值,考查逻辑推理能力及运算求解能力,属于中档题.
2022年高考数学新高考Ⅱ-19<-->2022年高考数学新高考Ⅱ-21
全网搜索"2022年高考数学新高考Ⅱ-20"相关
|

