2004年
解答题
(17)(本题满分12分)
已知数列![]() 的前n项和为
的前n项和为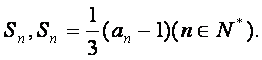
(Ⅰ)求![]() ;
;
(Ⅱ)求证数列![]() 是等比数列。
是等比数列。
(18)(本题满分12分)
在ΔABC中,角A、B、C所对的边分别为a、b、c,且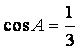 。
。
(Ⅰ)求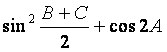 的值;
的值;
(Ⅱ)若![]() ,求bc的最大值。
,求bc的最大值。
(19)(本题满分12分)
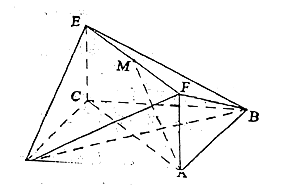
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
 AB=
AB=![]() ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。
(Ⅰ)求证AM∥平面BDE;
(Ⅱ)求证AM⊥平面BDF;
(Ⅲ)求二面角A—DF—B的大小;
解答 D
(20)(本题满分12分)
某地区有5个工厂,由于用电紧缺,规定每个工厂在一周内必须选择
某一天停电(选哪一天是等可能的)。假定工厂之间的选择互不影响。
(Ⅰ)求5个工厂均选择星期日停电的概率;
(Ⅱ)求至少有两个工厂选择同一天停电的概率。
(21)(本题满分12分)
已知a为实数,![]()
(Ⅰ)求导数![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 在[--2,2]
上的最大值和最小值;
在[--2,2]
上的最大值和最小值;
(Ⅲ)若![]() 在(--∞,--2]和[2,+∞)上都是递增的,求a的取值范围。
在(--∞,--2]和[2,+∞)上都是递增的,求a的取值范围。
(22)(本题满分14分)
解:已知双曲线的中心在原点,右顶点为A(1,0)点P、Q在双
曲线的右支上,支M(m,0)到直线AP的距离为1。
(Ⅰ)若直线AP的斜率为k,且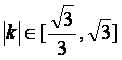 ,求实数m的
,求实数m的
取值范围;
(Ⅱ)当![]() 时,ΔAPQ的内心恰好是点M,求此双曲
时,ΔAPQ的内心恰好是点M,求此双曲
线的方程。
2005年
解答题
15.已知函数![]()
(Ⅰ) 求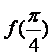 的值;
的值;
(Ⅱ) 设![]() ∈(0,
∈(0,![]() ),
),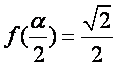 ,求sin
,求sin![]() 的值.
的值.
16.已知实数![]() 成等差数列,
成等差数列,![]() 成等比数列,且
成等比数列,且![]() ,求
,求![]()
17.袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是![]() ,
,
从B中摸出一个红球的概率为p.
(Ⅰ)
从A中有放回地摸球,每次摸出一个,共摸5次![]() 求
求
(i)恰好有3摸到红球的概率;(ii)第一次、第三次、第五次均摸到红球的概率.
(Ⅱ)
若A、B两个袋子中的球数之比为![]() ,将A、B中的球装在一起后,从中摸
,将A、B中的球装在一起后,从中摸
出一个红球的概率是![]() ,求p的值.
,求p的值.
18.如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=![]() PA,点O、D分别是AC、
PA,点O、D分别是AC、
PC的中点,OP⊥底面ABC.
(Ⅰ)求证![]() ∥平面
∥平面![]()
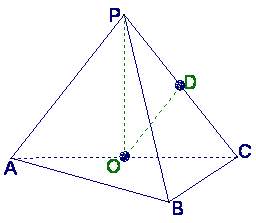
(Ⅱ) 求直线![]() 与平面PBC所成角的大小;
与平面PBC所成角的大小;
19.如图,已知椭圆的中心在坐标原点,焦点![]() 在x轴上,长轴A1A2的长为4,
在x轴上,长轴A1A2的长为4,
左准线![]() 与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
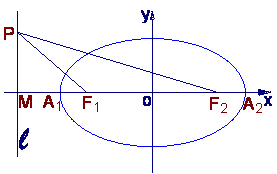 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P在直线上运动,求∠F1PF2的最大值.
20.函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|.
(Ⅲ)若在上是增函数,求实数的取值范围
2006
解答题
(17)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,
PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
(Ⅰ)求证:PB⊥DM;
(Ⅱ)求BD与平面ADMN所成的角.
(18)甲、乙两袋装有大小相同的红球和白球,甲袋装有2个红球,2个白球;
乙袋装有2个红球,n个白球.现从甲、乙两袋中各任取2个球.
(Ⅰ)若n=3,求取到的4个球全是红球的概率;
(Ⅱ)若取到的4个球中至少有2个红球的概率为,求n.
(19)如图,椭圆 (a>b>0)与过点A(2,0)、B(0,1)的直线有
且只有一个公共点T,且椭圆的离心率e=
(Ⅰ)求椭圆方程;
(Ⅱ)设Fl、F2分别为椭圆的左、右焦点,求证:|AT|2=|AF1|·|AF2|.
(20)设f(x)=3ax2+2bx+c,若a+b+c=0,f(0)f(1)>0,求证:
(Ⅰ)方程f(x)=0有实根;
(Ⅱ)-2<<-1;
(Ⅲ)设x1,x2是方程f(x)=0的两个实根,则≤|x1-x2|<.
2007
解答题
18.(本题14分)已知的周长为,且.
(I)求边的长;
(II)若的面积为,求角的度数.
19.(本题14分)已知数列中的相邻两项是关于的方程
的两个根,且.
(I)求,,,及()(不必证明);
(II)求数列的前项和.
20.(本题14分)在如图所示的几何体中,平面,平面,
,且,是的中点.
(I)求证:;
(II)求与平面所成的角的正切值.
21.(本题15分)如图,直线与椭圆交于两点,记的面积为.
(I)求在,的条件下,的最大值;
(II)当,时,求直线的方程.
22.(本题15分)已知.
(I)若,求方程的解;
(II)若关于的方程在上有两个解,求的取值范围,
并证明.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。