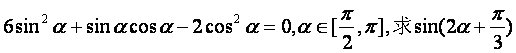2004年

解答题

17．（本小题满分12分）

       已知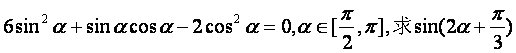的值.

  解答

18．（本小题满分12分）

     如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，AC与BD交于点E，

CB与CB₁交于点F.

（I）求证：A₁C⊥平BDC₁；

（II）求二面角B—EF—C的大小（结果用反三角函数值表示）.

　          解答

19．（本小题满分12分）

    如图，在Rt△ABC中，已知BC=a.若长为2a的线段PQ以点A为中点，

问的夹角θ取何值时的值最大？并求出这个最大值.

　　　　　　　　　　解答

20．（本小题满分12分）

直线的右支交于不同的两点A、B.

（Ⅰ）求实数k的取值范围；

（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？

若存在，求出k的值；若不存在，说明理由.

　解答

21．（本小题满分12分）

为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施

可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的

概率（记为P）和所需费用如下表：

预防方案可单独采用一种预防措施或联合采用几种预防措施，在总费用不超

过120万元的前提下，请确定一个预防方案，使得此突发事件不发生的概率最大.

 解答

22．（本小题满分14分）

已知的图象相切.

（Ⅰ）求b与c的关系式（用c表示b）；

（Ⅱ）设函数内有极值点，求c的取值范围.

 解答

2005年

解答题

17．（本小题满分12分）

  已知向量a=(，x+1)，b= (1-x，t)若函数=a·b在区间（-1，1）上

  是增函数，求t的取值范围

解答

18．（本小题满分12分）

       在△ABC中，已知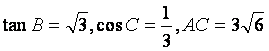，求△ABC的面积

解答

19．（本小题满分12分）

       设数列的前n项和为Sn=2n2，为等比数列，且

   （Ⅰ）求数列和的通项公式；

   （Ⅱ）设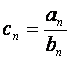，求数列的前n项和Tn

解答

20．（本小题满分12分）

    如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的，

    其中AB=4，BC=2，CC1=3，BE=1

   （Ⅰ）求BF的长；

   （Ⅱ）求点C到平面AEC1F的距离

    解答

21．（本小题满分12分）

      某会议室用5盏灯照明，每盏灯各使用灯泡一只，且型号相同.假定每盏灯

    能否正常照明只与灯泡的寿命有关，该型号的灯泡寿命为1年以上的概率为p1，

    寿命为2年以上的概率为p2.从使用之日起每满1年进行一次灯泡更换工作，只更换

    已坏的灯泡，平时不换

   （Ⅰ）在第一次灯泡更换工作中，求不需要换灯泡的概率和更换2只灯泡的概率；

   （Ⅱ）在第二次灯泡更换工作中，对其中的某一盏灯来说，求该盏灯需要更换灯泡

    的概率；

   （Ⅲ）当p1=0.8，p2=0.3时，求在第二次灯泡更换工作，至少需要更换4只灯泡

    的概率（结果保留两个有效数字）

解答

22．（本小题满分14分）

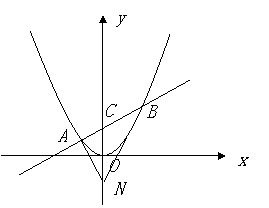
     设A、B是椭圆上的两点，点N（1，3）是线段AB的中点，

     线段AB的垂直平分线与椭圆相交于C、D两点

   （Ⅰ）确定的取值范围，并求直线AB的方程；

 （Ⅱ）试判断是否存在这样的，使得A、B、C、D四点在同一个圆上？并说明理由

解答

2006

解答题

16.（本小题满分12分）

设向量a=（sinx，cos x），b=（cosx，cosx），x∈R，函数f（x）=a（a+b）。

（Ⅰ）求函数f（x）的最大值与最小正周期；

（Ⅱ）求使不等式f（x）≥成立的x的取值集合。

解答

17．（本小题满分12分）

某单位最近组织了一次健身活动，活动分为登山组和游泳组，且每个职工至多参

加了其中一组，在参加活动的职工中，青年人占42.5%，中年人占47.5%，老年人

占10%。登山组的职工占参加活动总人数的，且该组中，青年人占50%，中年人

占40%，老年人占10%。为了了解各组不同年龄层次的职工对本次活动的满意程度，

现用分层抽样方法从参加活动的全体职工中抽取一个容量为200的样本，试确定

（Ⅰ）游泳组中，青年人、中年人、老年人分别所占的比例；

（Ⅱ）游泳组中，青年人、中年人、老年人分别应抽取的人数。

解答

18．（本小题满分12分）

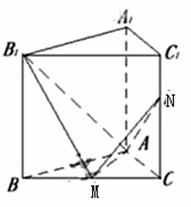
如图，已知正三棱柱ABC—A₁B₁C₁的侧棱长和底面边长为1，M是底面BC边上的中点，

N是侧棱CC₁上的点，且CN=2C₁N。

（Ⅰ）求二面角B₁—AM—N的平面角的余弦值；

（Ⅱ）求点B₁到平面AMN的距离。

解答

19．（本小题满分12分）

设函数f（x）=x³-ax²+bx+c在x=1处取得极值-2，试用c表示a和b，并求f（x）

的单调区间。

解答

20（本小题满分13分）

设数列{a_n}的前n项和为S_n，点（n，）（n∈N^*）均在函数y=3x-2的图像上。

（Ⅰ）求数列{a_n}的通项公式；

（Ⅱ）设b_n=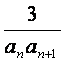，T_n是数列{b_n}的前n项和，求使得T_n＜对所有n∈N^*都成立的最小正整数m。

解答

21．（本小题满分14分）

设A、B分别为椭圆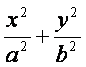=1（a，b＞0）的左、右顶点，椭圆长半轴的长等于焦距，

且x=4是它的右准线。

（Ⅰ）求椭圆的方程；

（Ⅱ）设P为右准线上不同于点（4，0）的任意一点，若直线AB，BP分别与椭圆相交于

异于A，B的M、N，证明点B在以MN为直径的圆内.

解答

2007年

解答题

16．（本小题满分12分）

已知函数，．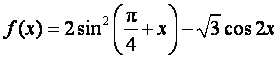

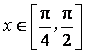（I）求的最大值和最小值；

（II）若不等式在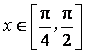上恒成立，求实数的取值范围．

 解答

17．（本小题满分12分）

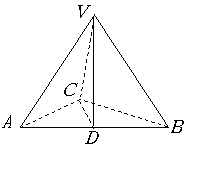如图，在三棱锥中，，，是的中点，且，

．

（I）求证：平面平面；

（II）试确定角的值，使得直线与

平面所成的角为．

 解答

18．（本小题满分12分）

某商品每件成本9元，售价为30元，每星期卖出432件，如果降低价格，销售量

可以增加，且每星期多卖出的商品件数与商品单价的降低值

（单位：元，）的平方成正比，已知商品单价降低2元时，

一星期多卖出24件．

（I）将一个星期的商品销售利润表示成的函数；

（II）如何定价才能使一个星期的商品销售利润最大？

 解答

19．（本小题满分12分）

设二次函数，方程的两根和满足．

（I）求实数的取值范围；

（II）试比较与的大小．并说明理由．

 解答

20．（本小题满分13分）

已知数列和满足：，，，（），

且是以为公比的等比数列．

（I）证明：；

（II）若，证明数列是等比数列；

（III）求和：．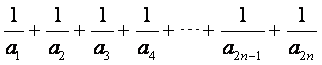

 解答

21．（本小题满分14分）

在平面直角坐标系中，过定点作直线与抛物线（）

相交于两点．

（I）若点是点关于坐标原点的对称点，求面积的最小值；

（II）是否存在垂直于轴的直线，使得被以为直径的圆截得的

弦长恒为定值？若存在，求出的方程；若不存在，说明理由．

（此题不要求在答题卡上画图）

 解答