2007年

解答题

17．（本小题满分12分）

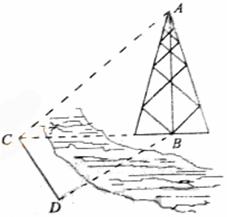
如图，测量河对岸的塔高时，可以选与塔底在同一水平面内的两个测点与．

现测得，并在点测得塔顶的仰角为，求塔高．

解答

18．（本小题满分12分）

如图，在三棱锥中，侧面与侧面均为等边三角形，，为中点．

（Ⅰ）证明：平面；

（Ⅱ）求二面角的余弦值．

解答

19．（本小题满分12分）

在平面直角坐标系中，经过点且斜率为的直线与椭圆有两个

不同的交点和．

（I）求的取值范围；

（II）设椭圆与轴正半轴、轴正半轴的交点分别为，是否存在常数，

使得向量与共线？如果存在，求值；如果不存在，请说明理由．

解答

20．（本小题满分12分）

如图，面积为的正方形中有一个不规则的图形，可按下面方法估计的

面积：在正方形中随机投掷个点，若个点中有个点落入中，

则的面积的估计值为，假设正方形的边长为2，

的面积为1，并向正方形中随机投掷个点，

以表示落入中的点的数目．

（I）求的均值；

（II）求用以上方法估计的面积时，的面积的估计值与实际值之差

在区间内的概率．

附表：

解答

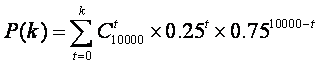
21．（本小题满分12分）

设函数

（I）若当时，取得极值，求的值，并讨论的单调性；

（II）若存在极值，求的取值范围，并证明所有极值之和大于．

解答

22．请考生在三题中任选一题作答，如果多做，则按所做的第一题记分．

作答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．

22．Ａ（本小题满分10分）选修4－1：几何证明选讲

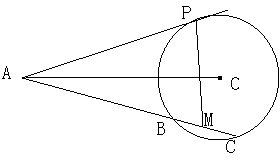
如图，已知是的切线，为切点，是的割线，与交于两点，

圆心在的内部，点是的中点．

（Ⅰ）证明四点共圆；

（Ⅱ）求的大小．

22．Ｂ（本小题满分10分）选修4－4：坐标系与参数方程

和的极坐标方程分别为．

（Ⅰ）把和的极坐标方程化为直角坐标方程；

（Ⅱ）求经过，交点的直线的直角坐标方程．

22．Ｃ（本小题满分10分）选修；不等式选讲

设函数．

（I）解不等式；

（II）求函数的最小值．

解答