2004年
解答题
17.(本小题满分12分)
求函数![]() 的取小正周期和取小值;
的取小正周期和取小值;
并写出该函数在![]() 上的单调递增区间。
上的单调递增区间。
18.(本小题满分12分)
设一汽车在前进途中要经过4个路口,汽车在每个路口遇到绿灯的
概率为![]() ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为![]() 。假定汽车只在遇到
。假定汽车只在遇到
红灯或到达目的地才停止前进,![]() 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求:
(1)![]() 的概率的分布列及期望E
的概率的分布列及期望E![]() ;
;
(2 ) 停车时最多已通过3个路口的概率。
19.(本小题满分12分)
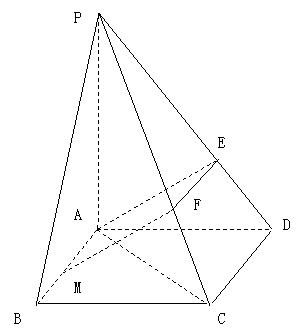
如图,四棱锥P-ABCD的底面是正方形,
![]()
(1) 证明MF是异面直线AB与PC的公垂线;
(2)
若![]() ,求直线AC与平面EAM所成角的正弦值。
,求直线AC与平面EAM所成角的正弦值。
20.(本小题满分12分)
设函数![]()
(1)
求导数![]() ;
并证明
;
并证明![]() 有两个不同的极值点
有两个不同的极值点![]() ;
;
(2)
若不等式![]() 成立,求
成立,求![]() 的取值范围。
的取值范围。
21.(本小题满分12分)
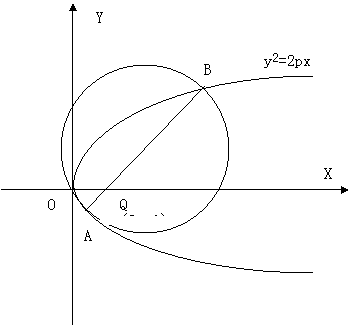
设![]() 是一常数,过点
是一常数,过点![]() 的直线与抛物线
的直线与抛物线![]() 交于相异
交于相异
两点A、B,以线段AB为直经作圆H(H为圆心)。试证抛物线顶点
在圆H的圆周上;并求圆H的面积最小时直线AB的方程。
![]()
22.(本小题满分14分)
设数列![]() 满足
满足![]()
(1)
证明![]() 对一切正整数n
成立;
对一切正整数n
成立;
(2)
令![]() ,判断
,判断![]() 的大小,并说明理由。
的大小,并说明理由。
2005年
解答题
17.(本小题满分13分)
若函数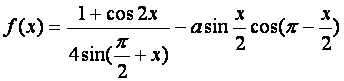 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
18.(本小题满分13分)
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;
有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券
中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值![]() (元)的概率分布列和期望
(元)的概率分布列和期望![]()
![]()
19.(本小题满分13分)
已知![]() ,讨论函数
,讨论函数![]() 的极值点的个数
的极值点的个数![]()
20.(本小题满分13分)
如图,在三棱柱ABC—A1B1C1中,AB⊥侧面BB1C1C,E为棱CC1上异于C、C1的一点,
EA⊥EB1,已知AB=![]() ,BB1=2,BC=1,∠BCC1=
,BB1=2,BC=1,∠BCC1=![]() ,求:
,求:
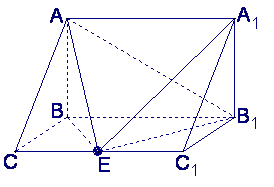 (Ⅰ)异面直线AB与EB1的距离;
(Ⅰ)异面直线AB与EB1的距离;
(Ⅱ)二面角A—EB1—A1的平面角的正切值.
21.(本小题满分12分)
已知椭圆C1的方程为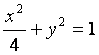 ,双曲线C2的左、右焦点分别为C1的左、右顶点,
,双曲线C2的左、右焦点分别为C1的左、右顶点,
而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线![]() 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2
的两个交点A和B满足![]() (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
22.(本小题满分12分)
数列{an}满足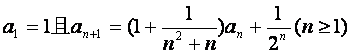 .
.
(Ⅰ)用数学归纳法证明:![]() ;
;
(Ⅱ)已知不等式![]() ,其中无理数
,其中无理数
e=2.71828….
2006
(17)(本小题满分13分)
设函数![]() (其中
(其中![]() )。且
)。且![]() 的图像在
的图像在
![]() 轴右侧的第一个最高点的横坐标是
轴右侧的第一个最高点的横坐标是![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)如果![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值;
的值;
(18)(本小题满分13分)
 某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该
某大厦的一部电梯从底层出发后只能在第18、19、20层可以停靠。若该
电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均
为![]() ,用
,用![]() 表示这5位乘客在20层下电梯的人数,求:
表示这5位乘客在20层下电梯的人数,求:
(Ⅰ)随即变量![]() 的分布列;
的分布列;
(Ⅱ)随即变量![]() 的期望;
的期望;
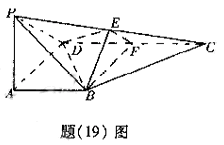
(19)(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角,
为直角,![]()
![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、CD的中点。
、CD的中点。
(Ⅰ)试证:![]() 平面
平面![]() ;
;
(Ⅱ)设PA=K·AB,且二面角![]() 的平面角大于
的平面角大于![]() ,求
,求![]() 的取值范围。
的取值范围。

(20)(本小题满分13分)
已知函数![]() ,其中
,其中![]() 为常数。
为常数。
(Ⅰ)若![]() ,讨论函数
,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,且
,且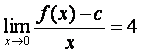 ,试证:
,试证:![]() ;
;
(21)(本小题满分12分)
已知定义域为![]() 的函数
的函数![]() 满足
满足![]() 。
。
(Ⅰ)若![]() ,求
,求![]() ;又若
;又若![]() ,求
,求![]() ;
;
(Ⅱ)设有且仅有一个实数![]() ,使得
,使得![]() ,求函数
,求函数![]() 的解析表达式;
的解析表达式;
(22)(本小题满分12分)
已知一列椭圆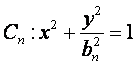 ,
,![]() 若椭圆
若椭圆![]() 上有一点
上有一点![]() ,
,
使![]() 到右准线
到右准线![]() 的距离
的距离![]() 是
是![]() 与
与![]() 的等差中项,
的等差中项,
其中![]() 分别是
分别是![]() 的左、右焦点。
的左、右焦点。

(Ⅰ)试证: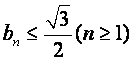 ;
;
(Ⅱ)取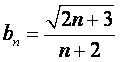 ,并用
,并用![]() 表示
表示![]() 的面积,
的面积,
试证:![]() 且
且![]()
2007年
解答题
17.(本小题满分13分,其中(Ⅰ)小问9分,(Ⅱ)小问4分.)
设![]() .
.
(Ⅰ)求![]() 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若锐角![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
18.(本小题满分13分,其中(Ⅰ)小问4分,(Ⅱ)小问9分)
某单位有三辆汽车参加某种事故保险,单位年初向保险公司缴纳每辆![]() 元的保险金,
元的保险金,
对在一年内发生此种事故的每辆汽车,单位可获![]() 元的赔偿(假设每辆车最多只赔
元的赔偿(假设每辆车最多只赔
偿一次),设这三辆车在一年内发生此种事故的概率分别为![]() ,
,![]() ,
,![]() ,且各车是否
,且各车是否
发生事故相互独立,求一年内该单位在此保险中:
(Ⅰ)获赔的概率;
(Ⅱ)获赔金额![]() 的分布列与期望.
的分布列与期望.
19.(本小题满分13分,其中(Ⅰ)小问8分,(Ⅱ)小问5分)
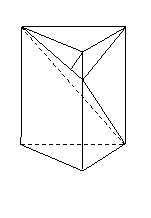 如题(19)图,在直三棱柱
如题(19)图,在直三棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]() ;
;
点![]() 分别在
分别在![]() ,
,![]() 上,且
上,且![]() ,
,
四棱锥![]() 与直三棱柱的体积之比为
与直三棱柱的体积之比为![]() .
.
(Ⅰ)求异面直线![]() 与
与![]() 的距离;
的距离;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的平面角的正切值.
的平面角的正切值.
20.(本小题满分13分,其中(Ⅰ),(Ⅱ),(Ⅲ)小问分别为6,4,3分.)
已知函数![]() 在
在![]() 处取得极值
处取得极值![]() ,其中
,其中![]() 为常数.
为常数.
(Ⅰ)试确定![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
21.(本小题满分12分,其中(Ⅰ)小问5分,(Ⅱ)小问7分.)
已知各项均为正数的数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,且
,且![]() ,
,![]() .
.
(Ⅰ)求![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 满足
满足![]() ,并记
,并记![]() 为
为![]() 的前
的前![]() 项和,求证:
项和,求证:
![]() .
.
22.(本小题满分12分,其中(Ⅰ)小问4分,(Ⅱ)小问8分.)
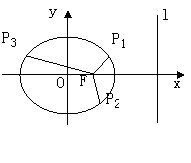
如题(22)图,中心在原点![]() 的椭圆的右焦点为
的椭圆的右焦点为![]() ,右准线
,右准线![]() 的方程为:
的方程为:![]() .
.
(1)求椭圆的方程;
 (Ⅱ)在椭圆上任取三个不同点
(Ⅱ)在椭圆上任取三个不同点![]() ,
,![]() ,
,![]() ,
,
使![]() ,
,
证明: 为定值,并求此定值.
为定值,并求此定值.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。