三、解答题

22．（本小题满分12分，其中（Ⅰ）小问4分，（Ⅱ）小问8分．）

如题（22）图，中心在原点的椭圆的右焦点为，右准线的方程为：．

（1）求椭圆的方程；

（Ⅱ）在椭圆上任取三个不同点，，，

使，

证明：为定值，并求此定值．

解：（I）设椭圆方程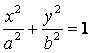为．

因焦点为，故半焦距．

又右准线的方程为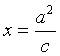，从而由已知

，

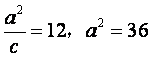因此，．

故所求椭圆方程为．

（II）记椭圆的右顶点为，并设（1，2，3），不失一般性，

假设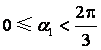，且，．

又设点在上的射影为，因椭圆的离心率，从而有

  ．

解得 ．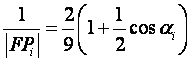

因此

，

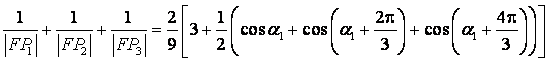而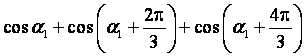

，

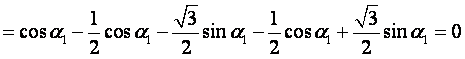故为定值．