三、解答题
20.(本小题满分13分,其中(Ⅰ),(Ⅱ),(Ⅲ)小问分别为6,4,3分.)
已知函数![]() 在
在![]() 处取得极值
处取得极值![]() ,其中
,其中![]() 为常数.
为常数.
(Ⅰ)试确定![]() 的值;
的值;
(Ⅱ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅲ)若对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(I)由题意知![]() ,因此
,因此![]() ,从而
,从而![]() .
.
又对![]() 求导得
求导得
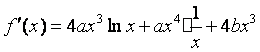
![]() .
.
由题意![]() ,因此
,因此![]() ,解得
,解得![]() .
.
(II)由(I)知![]() (
(![]() ),令
),令![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() ,此时
,此时![]() 为减函数;
为减函数;
当![]() 时,
时,![]() ,此时
,此时![]() 为增函数.
为增函数.
因此![]() 的单调递减区间为
的单调递减区间为![]() ,而
,而![]() 的单调递增区间为
的单调递增区间为![]() .
.
(III)由(II)知,![]() 在
在![]() 处取得极小值
处取得极小值![]() ,此极小值也是最小值,
,此极小值也是最小值,
要使![]() (
(![]() )恒成立,只需
)恒成立,只需![]() .
.
即![]() ,从而
,从而![]() ,
,
解得![]() 或
或![]() .
.
所以![]() 的取值范围为
的取值范围为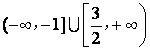 .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。