三、解答题
16.(本小题满分12分)
已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(I)求![]() 的取值范围;
的取值范围;
(II)求函数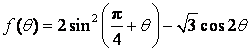 的最大值与最小值.
的最大值与最小值.
17.(本小题满分12分)
在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,
将数据分组如表:
|
分组 |
频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(I)在答题卡上完成频率分布表,并在给定的坐标系
中画出频率分布直方图;
(II)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]()
的概率是多少?
(III)统计方法中,同一组数据常用该组区间的中点值
(例如区间![]() 的中点值是
的中点值是![]() )作为代表.据此,
)作为代表.据此,
估计纤度的期望.
18.(本小题满分12分)
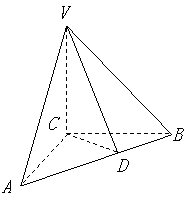
如图,在三棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,
,![]() 是
是![]() 的中点,且
的中点,且![]() ,
,
![]()
 .
.
(I)求证:平面![]()
![]() ;
;
(II)当解![]() 变化时,求直线
变化时,求直线![]() 与平面
与平面![]() 所成的角的取值范围.
所成的角的取值范围.
19.(本小题满分12分)
在平面直角坐标系![]() 中,过定点
中,过定点![]() 作直线与抛物线
作直线与抛物线![]() (
(![]() )相交于
)相交于![]() 两点.
两点.
(I)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(II)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?
为直径的圆截得的弦长恒为定值?
若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.

(此题不要求在答题卡上画图)
20.(本小题满分13分)
已知定义在正实数集上的函数![]() ,
,![]() ,其中
,其中![]() .
.
设两曲线![]() ,
,![]() 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用![]() 表示
表示![]() ,并求
,并求![]() 的最大值;
的最大值;
(II)求证:![]() (
(![]() ).
).
21.(本小题满分14分)
已知![]() 为正整数,
为正整数,
(I)用数学归纳法证明:当![]() 时,
时,![]() ;
;
(II)对于![]() ,已知
,已知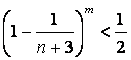 ,求证
,求证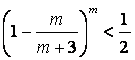 ,
,
求证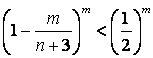 ,
,![]() ;
;
(III)求出满足等式![]() 的所有正整数
的所有正整数![]() .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。