三、解答题

17．（本小题满分13分，其中（Ⅰ）小问9分，（Ⅱ）小问4分．）

设．

（Ⅰ）求的最大值及最小正周期；

（Ⅱ）若锐角满足，求的值．

解答

18．（本小题满分13分，其中（Ⅰ）小问4分，（Ⅱ）小问9分）

某单位有三辆汽车参加某种事故保险，单位年初向保险公司缴纳每辆元的保险金，

对在一年内发生此种事故的每辆汽车，单位可获元的赔偿（假设每辆车最多只赔

偿一次），设这三辆车在一年内发生此种事故的概率分别为，，，且各车是否

发生事故相互独立，求一年内该单位在此保险中：

（Ⅰ）获赔的概率；

（Ⅱ）获赔金额的分布列与期望．

解答

19．（本小题满分13分，其中（Ⅰ）小问8分，（Ⅱ）小问5分）

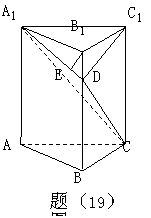如题（19）图，在直三棱柱中，

，，；

点分别在，上，且，

四棱锥与直三棱柱的体积之比为．

（Ⅰ）求异面直线与的距离；

（Ⅱ）若，求二面角的平面角的正切值．

解答

20．（本小题满分13分，其中（Ⅰ），（Ⅱ），（Ⅲ）小问分别为6，4，3分．）

已知函数在处取得极值，其中为常数．

（Ⅰ）试确定的值；

（Ⅱ）讨论函数的单调区间；

（Ⅲ）若对任意，不等式恒成立，求的取值范围．

解答

21．（本小题满分12分，其中（Ⅰ）小问5分，（Ⅱ）小问7分．）

已知各项均为正数的数列的前项和满足，且，．

（Ⅰ）求的通项公式；

（Ⅱ）设数列满足，并记为的前项和，求证：

．

解答

22．（本小题满分12分，其中（Ⅰ）小问4分，（Ⅱ）小问8分．）

如题（22）图，中心在原点的椭圆的右焦点为，右准线的方程为：．

（1）求椭圆的方程；

（Ⅱ）在椭圆上任取三个不同点，，，

使，

证明：为定值，并求此定值．

解答