三、解答题

15．（本小题共12分）

记关于的不等式的解集为，不等式的解集为．

（I）若，求；

（II）若，求正数的取值范围．

解答

16．（本小题共13分）

数列中，（是常数，），且成公比

不为的等比数列．

（I）求的值；

（II）求的通项公式．

解答

17．（本小题共14分）

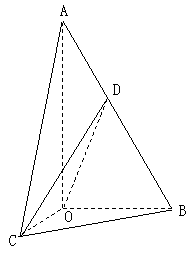
如图，在中，，斜边．可以通过以

直线为轴旋转得到，且二面角的直二面角．是的中点．

（I）求证：平面平面；

（II）求异面直线与所成角的大小．

解答

18．（本小题共12分）

某条公共汽车线路沿线共有11个车站（包括起点站和终点站），在起点站开出的一辆

公共汽车上有6位乘客，假设每位乘客在起点站之外的各个车站下车是等可能的．求：

（I）这6位乘客在其不相同的车站下车的概率；

（II）这6位乘客中恰有3人在终点站下车的概率；

解答

19．（本小题共14分）

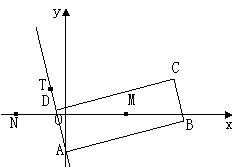如图，矩形的两条对角线相交于点，边所在直线的方程

为点在边所在直线上．

（I）求边所在直线的方程；

（II）求矩形外接圆的方程；

（III）若动圆过点，且与

矩形的外接圆外切，求动圆的圆心的轨迹方程．

解答

20．（本小题共14分）

已知函数与的图象相交于，，，分别

是的图象在两点的切线，分别是，与轴的交点．

（I）求的取值范围；

（II）设为点的横坐标，当时，写出以为自变量的函数式，

并求其定义域和值域；

（III）试比较与的大小，并说明理由（是坐标原点）．

解答