的三个内角为A、B、C，求当A为何值时
取得最大值，解答题
全国卷Ⅰ(理)
（17）（本小题满分12分）
的三个内角为A、B、C，求当A为何值时取得最大值，
并求出这个最大值。
全国卷Ⅱ(理)
（17）（本小题满分１２分）
已知向量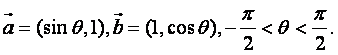
（I）若
求
（II）求
的最大值。
北京卷(理)
（15）（本小题共12分）
已知函数f（x）=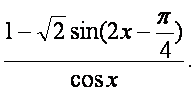
（Ⅰ）求f（x）的定义域；
（Ⅱ）设α是第四象限的角，且tanα=－
求f（α）的值.
天津卷(理)
(17)(本小题满分12分)
如图，在△ABC中，AC=2，BC=l，cosC=
．
(Ⅰ)求AB的值；
(Ⅱ)求sin(2A+C)的值．
上海卷(理)
17．（本题满分12分）
求函数
＝2
＋
的值域和最小正周期．
辽宁卷
(17) (本小题满分12分)
已知函数
，
.求:
(I)
函数
的最大值及取得最大值的自变量
的集合；
(II)
函数的单调增区间.
江苏卷
（17）（本小题满分12分，第一小问满分5分，第二小问满分7分）
已知三点P（5，2）、
（－6，0）、
（6，0）.
（Ⅰ）求以
、
为焦点且过点P的椭圆的标准方程；
（Ⅱ）设点P、
、
关于直线y＝x的对称点分别为
、
、
，
求以
、
为焦点且过点
的双曲线的标准方程。
浙江卷(理)
（15）如图，函数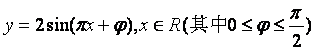
的图象与y轴交于点（0，1）
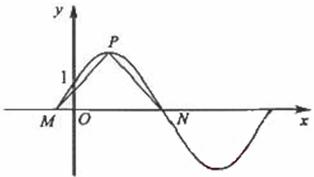
（Ⅰ）求
的值；
（Ⅱ）设P是图象上的最高点，M、N是图象与x轴的交点，求
与
的夹角。
福建卷(理)
（17）（本小题满分12分）
已知函数
（I）求函数
的最小正周期和单调增区间；
（II）函数
的图象可以由函数
的图象经过怎样的变换得到？
湖北卷(理)
16．（本小题满分12分）
设函数
·（b+c）,其中向量a=(sinx,—cosx)，b=(sinx,—3cosx),
c=(—cosx,sinx),x
。
（Ⅰ）求函数f(x)的最大值和最小正周期；
（Ⅱ）将函数y=f(x)的图像按向量d平移，使平移后得到的图象关于坐标
原点成中心对称，求长度最小的d。
湖南卷(理)
16．（本小题满分12分）
如图3，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=α，∠ABC=β.
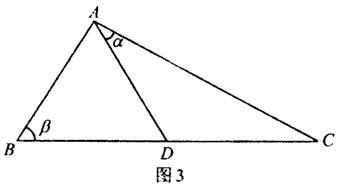
（Ⅰ）证明：sinα+cos2β=0；
（Ⅱ）若AC=
DC，求β的值.
广东卷
15．（本小题满分14分）
已知函数
（Ⅰ）求f(x)的最小正周期：
（Ⅱ）求f(x)的最大值和最小值：
（Ⅲ）若
求sin2
的值。
重庆卷(理)
（17）（本小题满分13分）
设函数
（其中
）。且
的图像在
轴右侧的第一个最高点的横坐标是
。
（Ⅰ）求
的值；
（Ⅱ）如果
在区间
上的最小值为
，求
的值；
山东卷(理)
17.(本小题满分12分)
已知函数F(x)=Asin2(ωx+φ)(A＞0，ω＞0，0＜φ＜
)，且y＝f(x)的最大值为2，
其图象相邻两对称轴间的距离为2，并过点(1，2)．
(Ⅰ)求φ；
(Ⅱ)计算f(1)+f(2)+…+f(2008)．
江西卷(理)
17．(本小题满分12分)
已知函数f(x)=x3+ax2+bx+c在x=-
与x=1时都取得极值．
(1)求a、b的值及函数f(x)的单调区间；
(2)若对x∈[－1，2]，不等式f(x)＜c2恒成立，求c的取值范围．
陕西卷(理)
（17）（本小题满分１２分）
已知函数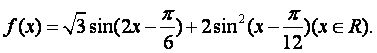
（I）求函数
的最小正周期；
（II）求使函数
取得最大值的
集合。
四川卷(理)
（17）（本大题满分12分）
数列
的前
项和记为
（Ⅰ）求
的通项公式；
（Ⅱ）等差数列
的各项为正，其前
项和为
，且
，
又
成等比数列，求
安徽卷(理)
（17）（本小题满分12分）
已知
<
<
,tan+cot=
。
（Ⅰ）求tan
的值
（Ⅱ）求
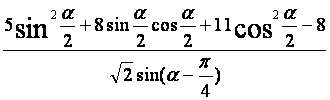的值。
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。