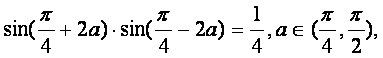解答题

(17)(本小题满分12分)

   已知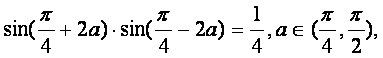求的值.

  解答

(19) (本小题满分12分)

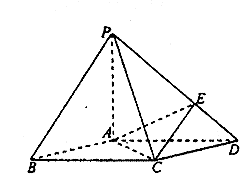
如图,在底面是菱形的四棱锥P—ABCD中,

     点E在PD上,且PE:ED= 2: 1.

     (Ⅰ)证明 PA⊥平面ABCD;

(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小:

(Ⅲ)在棱PC上是否存在一点F, 使BF∥平面AEC?证明你的结论.

                                  解答

(20)(本小题满分12分)

已知函数其中a≤0,e为自然对数的底数.

  (Ⅰ)讨论函数f(x)的单调性;

(Ⅱ)求函数f(x)在区间[0,1]上的最大值.

 解答

(21)(本小题满分12分)

 如图,过抛物线x²=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线

交于A、B两点，点Q是点P关于原点的对称点。

  (Ⅰ)设点P分有向线段所成的比为λ，证明

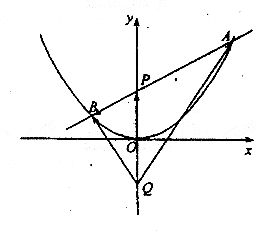(Ⅱ)设直线AB的方程是x—2y+12=0,过A、B两点的圆C与抛物线在点A处

有共同的切线，求圆C的方程。

                                             解答

（22）（本小题满分14分）

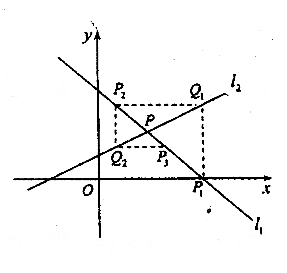
如图，直线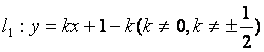与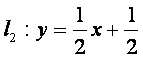相交于点P。直线

与x轴交于点P₁，过点P₁作x轴的垂线交直线于点Q₁，过点Q₁作y轴的

垂线交直线于点P₂，过点P₂作x轴的垂线交直线于点Q₂，…，这样

一直作下去，可得到一系列点P₁，Q₁，P₂，Q₂，…。点P_n（n=1,2,…）

的横坐标构成数列。

  (Ⅰ)证明

(Ⅱ)求数列的通项公式；

(Ⅲ)比较与的大小。

 解答