解答题

全国卷Ⅰ(文)

20．（本小题满分12分）

从10位同学（其中6女，4男）中随机选出3位参加测验.每位女同学能通过

测验的概率均为，每位男同学能通过测验的概率均为.试求：

（I）选出的3位同学中，至少有一位男同学的概率；

（II）10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.

 解答

全国卷Ⅱ(文)

20．（本小题满分12分）

   如图，直三棱柱ABC—A₁B₁C₁中，∠ACB=90°，AC=1，CB=，

侧棱AA₁=1，侧面AA₁B₁B的两条对角线交点为D，B₁C₁的中点为M.

（Ⅰ）求证CD⊥平面BDM；

（Ⅱ）求面B₁BD与面CBD所成二面角的大小.

           解答

全国卷Ⅲ(文)

20．（本小题满分12分）某村计划建造一个室内面积为800的矩形蔬菜温室。

在温室内，沿左．右两侧与后侧内墙各保留1宽的通道，沿前侧内墙保留3宽

的空地。当矩形温室的边长各为多少时？蔬菜的种植面积最大。最大种植面积是多少？

解答

全国卷Ⅳ(文)

20．（本小题满分12分）

   某同学参加科普知识竞赛，需回答3个问题.竞赛规则规定：答对

第一、二、三问题分别得100分、100分、200分，答错得零分.假设这

名同学答对第一、二、三个问题的概率分别为0.8、0.7、0.6，且各题

答对与否相互之间没有影响.

（Ⅰ）求这名同学得300分的概率；

（Ⅱ）求这名同学至少得300分的概率.

解答

天津卷(文)

20.（本小题满分12分）

设是一个公差为的等差数列，它的前10项和

且，，成等比数列。

（1）证明；（2）求公差的值和数列的通项公式。

解答

辽宁卷

20．（本小题满分12分）

甲方是一农场，乙方是一工厂. 由于乙方生产须占用甲方的资源，因此

甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付

甲方的情况下，乙方的年利润x（元）与年产量t（吨）满足函数关系

.若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格），

   （1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方

获得最大利润的年产量；

   （2）甲方每年受乙方生产影响的经济损失金额（元），在乙方

按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，

应向乙方要求的赔付价格s是多少？

解答

江苏卷

20.设无穷等差数列{a_n}的前n项和为S_n.

(Ⅰ)若首项  EQ \F(3,2) ，公差，求满足的正整数k；

(Ⅱ)求所有的无穷等差数列{a_n}，使得对于一切正整数k都有成立.

解答

浙江卷(文)

（20）（本题满分12分）

某地区有5个工厂，由于用电紧缺，规定每个工厂在一周内必须选择

某一天停电（选哪一天是等可能的）。假定工厂之间的选择互不影响。

    （Ⅰ）求5个工厂均选择星期日停电的概率；

 （Ⅱ）求至少有两个工厂选择同一天停电的概率。

解答

福建卷(文)

20．（本小题满分12分）

某企业2003年的纯利润为500万元，因设备老化等原因，企业的生产能

力将逐年下降.若不能进行技术改造，预测从今年起每年比上一年纯利

润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，

预测在未扣除技术改造资金的情况下，第n年（今年为第一年）的利润

为500(1+)万元（n为正整数）.

（Ⅰ）设从今年起的前n年，若该企业不进行技术改造的累计纯利润为

A_n万元，进行技术改造后的累计纯利润为B_n万元（须扣除技术改造资金），

求A_n、B_n的表达式；

（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的

累计纯利润超过不进行技术改造的累计纯利润？

  解答

湖北卷(文)

20．（本小题满分12分）

直线的右支交于不同的两点A、B.

（Ⅰ）求实数k的取值范围；

（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？

若存在，求出k的值；若不存在，说明理由.

　解答

湖南卷(文)

20．（本小题满分12分）

    已知数列{a_n}是首项为a且公比q不等于1的等比数列，S_n是其前n项的和，

a₁,2a₇,3a₄ 成等差数列.

（I）证明  12S₃,S₆,S₁₂-S₆成等比数列；

（II）求和T_n=a₁+2a₄+3a₇+…+na_3n-2.

解答

重庆卷(文)

20．（本小题满分12分）

     某工厂生产某种产品，已知该产品的月生产量（吨）与每吨产品的价格

（元/吨）之间的关系式为：,且生产x吨的成本为（元）。

问该产每月生产多少吨产品才能使利润达到最大？最大利润是多少？（利润=收入─成本）

解答

北京卷(文)

（18）（本小题满分14分）

    函数定义在［0，1］上，满足且，在每个区间

（1，2……）上，的图象都是平行于x轴的直线的一部分。

    （I）求及，的值，并归纳出的表达式

    （II）设直线，，x轴及的图象围成的矩形的面积

为（1，2……），求及的值

     解答

上海卷(文)

20、(本题满分14分) 第1小题满分6分, 第2小题满分8分

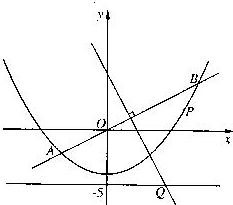如图, 直线y=x与抛物线y=x²－4交于A、B两点, 线段AB的垂直

平分线与直线y=－5交于Q点.

 (1) 求点Q的坐标；

(2) 当P为抛物线上位于线段AB下方

(含A、B) 的动点时, 求ΔOPQ面积的最大值.

解答 

广东卷

20 (12分)某中心接到其正东、正西、正北方向三个观测点的报告：正西、

正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观

测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生

的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)

 解答