福建(理)
一、选择题(每题5分)
(1)设![]() 则复数
则复数![]() 为实数的充要条件是(
)
为实数的充要条件是(
)
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(4)已知全集![]() 且
且![]()
则![]() 等于(
)
等于(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、天空题(每题4分)
(13)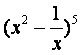 展开式中
展开式中![]() 的系数是_____(用数字作答)。
的系数是_____(用数字作答)。
三、解答题
(19)(本小题满分12分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量![]() (升)关于行驶
(升)关于行驶
速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:
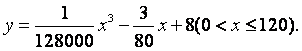 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
浙江(理)
一、选择题(每小题5分)
(1)设集合A={x|-1≤x≤2},B={x|0≤x≤4},则A![]() B=()
B=()
(A)[0,2] (B)[1,2] (C)[0,4] (D)[1,4]
(2)已知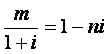 ,其中m,n是实数,i是虚数单位,则m+ni=()
,其中m,n是实数,i是虚数单位,则m+ni=()
(A)1+2i (B)1-2i (C)2+i (D)2-i
二、填空题(每小题4分)
(13)设向量a,b,c满足a+b+c=0,(a-b)![]() c,a
c,a![]() b,若|a|
=1,
b,若|a|
=1,
则![]() 的值是_________.
的值是_________.
天津(理)
一、选择题(每小题5分)
(1)i是虚数单位,![]() =()
=()
(A)
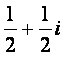 (B)
(B)
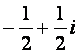 (C)
(C)
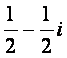 (D)
(D)
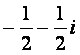
(4)设集合M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是“a∈N”的()
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(5)将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放人
每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有()
(A)10种 (B)20种 (C)36种 (D)52种
二、填空题(每小题4分)
(12)设向量![]() 与
与![]() 的夹角为θ,且
的夹角为θ,且![]() =(3,3),2
=(3,3),2![]() -
-![]() =(-l,1),则cosθ=___.
=(-l,1),则cosθ=___.
江苏
一、选择题(每小题5分)
(7)若A、B、C为三个集合,![]() ,则一定有()
,则一定有()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题5分)
(13)今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球
排成一列有 种不同的方法(用数字作答)。
辽宁(理)
一、选择题(每题5分)
(1) 设集合![]() ,则满足
,则满足![]() 的集合B的个数是(
)
的集合B的个数是(
)
(A)1 (B)3 (C)4 (D)8
(5)
设®是R上的一个运算,A是R的非空子集,若对任意![]()
有![]() ®
®![]()
![]() ,则称A对运算®封闭,下列数集对加法、减法、乘法和除法
,则称A对运算®封闭,下列数集对加法、减法、乘法和除法
(除数不等于零)四则运算都封闭的是( )
(A)自然数集 (B)整数集 (C)有理数集 (D)无理数集
二、填空题(每题4分)
(14)
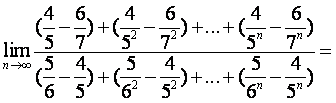 _____________
_____________
(15) 5名乒乓球队员中,有2名老队员和3名新队员.现从中选出3名队员排成1、2、3号
参加团体比赛,
则入选的3名队员中至少有一名老队员,且1、2号中至少有1名新队员的排法有_______种.
(以数作答)
重庆(理)
一、选择题(每小题5分)
(1)已知集合![]() ,
,![]() ,
,![]() ,则(CUA)∪(CUB)()
,则(CUA)∪(CUB)()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(7)与向量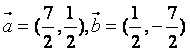 的夹角相等,且模为1的向量是()
的夹角相等,且模为1的向量是()
(A)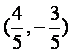 (B)
(B)![]() 或
或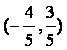
(C)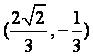 (D)
(D)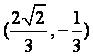 或
或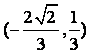
(8)将5名实习教师分配到高一年级的3个班实习,每班至少1名,最多2名,
则不同的分配方案有()
(A)30种 (B)90种 (C)180种 (D)270种
二、填空题(每小题4分)
(11)复数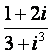 的值是
。
解答
的值是
。
解答
(12)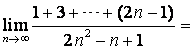 。解答
。解答
湖南(理)
一、选择题(每题5分)
5.已知|![]() |=2|
|=2|![]() |≠0,且关于x的方程x2+|
|≠0,且关于x的方程x2+|![]() |x+
|x+![]() ·
·![]() =0有实根,则
=0有实根,则![]() 与
与![]() 的夹角的
的夹角的
取值范围是( )
A.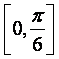 B.
B.
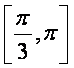 C.
C.
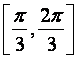 D.
D.
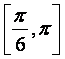
6.某外商计划在4个候选城市投资3个不同的项目,且在同一个城市投资的项目不超
过2个,则该外商不同的投资方案有( )
A.16种 B.36种 C.42种 D.60种
二、填空题(每题4分)
11.若(ax-1)5的展开式中x3的系数是-80,则实数a的值是 .
三、解答题
20.(本小题满分14分)
对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为:
1-![]() )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案
甲:一次清洗;方案乙:分两次清洗.该物体初次清洗后受残留水等因素影响,其
质量变为a(1≤a≤3).设用x单位质量的水初次清洗后的清洁度是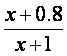 (x>a-1),用
(x>a-1),用
y单位质量的水第二次清洗后的清洁度是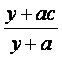 ,其中c(0.8<c<0.99)是该物体初次清
,其中c(0.8<c<0.99)是该物体初次清
洗后的清洁度.
(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量,并比较哪一种方案用水量较少;
(Ⅱ)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水
量最少?并讨论a取不同数值时对最少总用水量多少的影响.
湖北(理)
一、选择题(每题5分)
5.在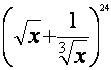 的展开式中,x的幂的指数是整数的项共有(
)
的展开式中,x的幂的指数是整数的项共有(
)
A.3项 B.4项 C.5项 D.6项
8.有限集合S中元素的个数记作card(S).设A、B都为有限集合,给出下列命题:
①![]() 的充要条件是card(
的充要条件是card(![]() )=card(A)+card(B);
)=card(A)+card(B);
②![]() 的必要条件是card(A)≤card(B);
的必要条件是card(A)≤card(B);
③![]() 的充分条件是card(A)≤card(B);
的充分条件是card(A)≤card(B);
④A=B的充要条件是card(A)= card(B)。
其中真命题的序号是( )
A.③、④ B.①、② C.①、④ D.②、③
10.关于x的方程(x2-1)2-│x2-1│+k=0,给出下列四个命题:
①存在实数k,使得方程恰有2个不同的实根;
②存在实数k,使得方程恰有4个不同的实根;
③存在实数k,使得方程恰有5个不同的实根;
④存在实数k,使得方程恰有8个不同的实根。
其中假命题的个数是( )
A.0 B.1 C.2 D.3
二、填空题(每题5分)
11.设x、y为实数,且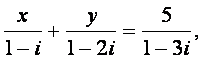 则x+y=_____________。
则x+y=_____________。
14.某工程队有6项工程需要先后单独完成,其中工程乙必须在工程甲完成后才
能进行,工程丙必须在工程乙完成后才能进行,又工程丁必须在工程丙完成后立
即进行,那么安排这6项工程的不同排法种数是____________。(用数字作答)
15.将杨辉三角中的每一个数![]() 都换成分数
都换成分数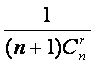 ,就得到一个如图所示的
,就得到一个如图所示的
分数三角形,称为
莱布尼茨三角形,从莱布尼茨三角形可看出

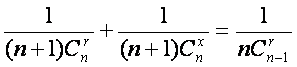 ,其中x=______________.
,其中x=______________.
令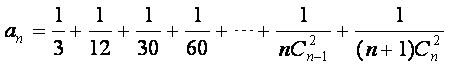 ,则
,则![]()
广东
一、选择题(每题5分)
2.若复数z满足议程z2 +2=0,则z3=
A.![]() B.
B.![]() C.
C.![]() D.+2
D.+2![]()
4.如图1所示,D是△ABC的边AB上的中点,则向量![]() =(A)
=(A)
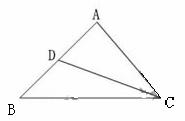
A.![]() B.
B.![]()
C.
![]() D.
D.
![]()
10、对于任意的两个实数对(a,b)和(c,d),规定:(a,b)=(c,d),当且仅
当a=c,b=d;运算“![]() ”为:(a,b)
”为:(a,b)![]() (c,d)=(ac-bd,bc+ad),运算“
(c,d)=(ac-bd,bc+ad),运算“![]() ”为:
”为:
(a,b)![]() (c,d)=(a+c,b+d),设p、q
(c,d)=(a+c,b+d),设p、q![]() 若(1,2)
若(1,2)![]() (p,q)=(5,0)
(p,q)=(5,0)
则(1,2)![]() (p,q)=()
(p,q)=()
A、(4,0) B、(2,0) C、(0,2) D、(0、-4)
11.![]()
![]() __________________。解答
__________________。解答
14.在德国不莱梅举行的第48届世乒赛期间,某商场橱窗里用同样的乒乓球对
成若干堆“正三棱锥”形的展品,其中第一堆只有一层,就一个球,第2、3、4,
一堆最底层(第一层)分别按图所示方向固定摆放,从第二层开始。每层的小球
自然垒放在下一层之上,第n堆第n层就放一个乒乓球,以f(n)表示n堆的乒乓球
总数,则f(3)=___________; f(n)__________(答案用n表示)
北京(理)
一、选择题(每题5分)
(1)在复平面内,复数![]() 对应的点位于( )
对应的点位于( )
(A)第一象限 (B)第二象限
(C)第三象限 (D)第四象限
(3)在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字
之和为奇数的共有( )
(A)36个 (B)24个
(C)18个 (D)6个
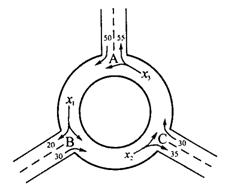
(8)下图为某三岔路口交通环岛的简化模型.在某高峰时段,单位时间进出路
口A,B,C的机动车辆数如图所示,图中x1,x2,x3分别表示该时段单位时间
通过路段![]() ,
,![]() ,
,![]() 的机动车辆数(假设:单位时间内,在上述路段中,同一路
的机动车辆数(假设:单位时间内,在上述路段中,同一路
段上驶入与驶出的车辆数相等),则( )
(A)x1>x2>x3 (B)x1>x3>x2
(C)x2>x3>x1 (D)x3>x2>x1
二、填空题(每题5分)
(9)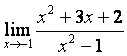 的值等于___________.
的值等于___________.
(10)在(![]() )7的展开式中,x2的系数是____________.(用数字作答)
)7的展开式中,x2的系数是____________.(用数字作答)
上海(理)
一、填空题(每小题4分)
1.已知集合A=![]() -1,3,2
-1,3,2![]() -1
-1![]() ,集合B=
,集合B=![]() 3,
3,![]()
![]() .若B
.若B![]() A,
A,
则实数![]() =
.解答
=
.解答
4.计算: =
.解答
=
.解答
5.若复数![]() 同时满足
同时满足![]() -
-![]() =2
=2![]() ,
,![]() =
=![]() (
(![]() 为虚数单位),则
为虚数单位),则![]() =
.
=
.
山东(理)
一、选择题(每小题5分)
1.定义集合运算:A⊙B={z|z=xy(x+y),x∈A,y∈B}.设集合A={0,1},
B={2,3},则集合A⊙B的所有元素之和为()
(A)0 (B)6 (C)12 (D)18
5.设向量a=(1,-3),b=(-2,4),c=(-1,-2).若表示向量4a、4b-2c、2(a-c)、d
的有向线段首尾相接能构成四边形,则向量d为()
(A)(2,6) (B)(-2,6)
(C)(2,-6) (D)(-2,-6)
9.已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素
构成空间直角坐标系中点的坐标,则确定的不同点的个数为()
(A)33 (B)34 (C)35 (D)36
二、填空题(每小题4分)
13.若![]()
 =1,则常数a=________.
解答
=1,则常数a=________.
解答
16.下列四个命题中,真命题的序号有________(写出所有真命题的序号).
①将函数y=|x+1|的图象按向量v=(-1,0)平移,得到的图象对应的函数
表达式为y=|x|
②圆x2+y2+4x+2y+1=0与直线y=![]() x相交,所得弦长为2
x相交,所得弦长为2
③若sin(α+β)=![]() ,sin(α-β)=
,sin(α-β)=![]() ,则tanαcotβ=5
,则tanαcotβ=5
④如图,已知正方体ABCD-A1B1C1D1,P为底面ABCD内一动点,
P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是
抛物线的一部分

江西(理)
一、选择题(每题5分)
1.已知集合M={x| },N={y|y=3x2+1,x∈R},则M∩N等于(
)
},N={y|y=3x2+1,x∈R},则M∩N等于(
)
A. ![]() B.{x|x≥1}
C.{x|x>1} D.{x|x≥1或x<0}
B.{x|x≥1}
C.{x|x>1} D.{x|x≥1或x<0}
2.已知复数z满足(![]() +3i)z=3i,则z等于(
)
+3i)z=3i,则z等于(
)
A. i
B.
i
B.
 i
C.
i
C. D.
D. i
i
8.在(x-![]() )2006的二项展开式中,含x的奇次幂的项之和为S,当x=
)2006的二项展开式中,含x的奇次幂的项之和为S,当x=![]() 时,
时,
S等于( )
A.23008 B.-23008 C.23009 D.-23009
陕西(理)
一、选择题(每小题5分)
1.已知集合![]() 集合
集合![]() 则
则![]() 等于()
等于()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2.复数 等于()
等于()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.
 等于()
等于()
(A)0 (B)![]() (C)
(C)![]() (D)
(D)![]()
9.已知非零向量![]() 与
与![]() 满足
满足 且
且 则
则![]() 为()
为()
(A)等边三角形 (B)直角三角形
(C)等腰非等边三角形 (D)三边均不相等的三角形
二、填空题(每小题4分)
16.某校从8名教师中选派4名教师同时去4个边远地区支教(每地1人),
其中甲和乙不同去,甲和丙只能同去或同不去,则不同的选派方案共
有_____种(用数字作答)。解答
安徽(理)
一、选择题(每小题5分)
(1)
复数 等于(
)
等于(
)
(A)i (B)-i (C)![]() (D)
(D)![]()
(2)设集合A=![]() x||x-2|
x||x-2|![]() ,x
,x![]() ,B={y|y=-x2,
-1
,B={y|y=-x2,
-1![]() },则CR(A∩B)等于(
)
},则CR(A∩B)等于(
)
(A)R (B){x|x![]() } (C){0} (D)
} (C){0} (D)![]()
二、填空题(每题4分)
(13)设常数a>o,(ax2+![]() )4展开式中x3的系数为
)4展开式中x3的系数为![]() ,
,
则![]() (a+a2+...+an)=
。
(a+a2+...+an)=
。
(14)在![]() ABCD中,
ABCD中,![]() ,
,![]() ,
,![]() 为BC的中点,
为BC的中点,
则![]() = ______。(用a,b表示)
= ______。(用a,b表示)
四川(理)
一、选择题(每小题5分)
(1)已知集合![]() ,集合
,集合![]() ,则集合
,则集合![]()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)复数(1-i)3的虚部为()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(7)
如图,已知正六边形![]() ,下列向量的数量积中最大的是()
,下列向量的数量积中最大的是()

(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二、填空题(每小题4分)
(14)设离散型随机变量![]() 可能取的值为1,2,3,4。
可能取的值为1,2,3,4。![]() ,
,
又![]() 的数学期望
的数学期望![]() ,则
,则![]() ________________;解答
________________;解答
(16)非空集合![]() 关于运算
关于运算![]() 满足:(1)对任意
满足:(1)对任意![]() ,都有
,都有![]() ;
;
(2)存在![]() ,使得对一切
,使得对一切![]() ,都有
,都有![]() ,则称
,则称![]() 关于
关于
运算![]() 为“融洽集”;现给出下列集合和运算:
为“融洽集”;现给出下列集合和运算:
①![]() ②
②![]()
③![]() ④
④![]()
⑤![]()
其中![]() 关于运算
关于运算![]() 为“融洽集”的是________________;
解答
为“融洽集”的是________________;
解答
(写出所有“融洽集”的序号)
全国卷(Ⅰ)理
一.选择题(每题5分)
(1)设集合M={x│x2-x<0},N={x││x│<2},则( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(4)如果复数(m2+i)(1+mi)是实数,则实数![]()
(A)1
(B)-1
(C)![]() (D)-
(D)-![]()
(11)用长度分别为2、3、4、5、6(单位:cm)的5根细木棒围成一个三角形
(允许连接,但不允许折断),能够得到的三角形的最大的面积为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(12)设集合![]() 选择
选择![]() 的两个非空子集A和B,要使B中最小的数大于A中
的两个非空子集A和B,要使B中最小的数大于A中
的最大的数,则不同的选择方法共有( )
(A)50种(B)49种(C)48种(D)47种
(15)安排7位工作人员在5月1日至5月7日值勤班,每人值班一天,其中甲、乙二人
都不安排在5月1日和2日。不同的安排方法共有 种。(用数字作答)
全国卷(Ⅱ)理
一、选择题(每小题5分)
(1)已知集合![]() ,则
,则![]()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
三、解答题
(17)(本小题满分12分)
已知向量
(I)若![]() 求
求![]()
(II)求![]() 的最大值。
的最大值。
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。