三、解答题

20．(本小题满分14分)

对1个单位质量的含污物体进行清洗，清洗前其清洁度(含污物体的清洁度定义为：

1-)为0.8，要求洗完后的清洁度是0.99．有两种方案可供选择，方案

甲：一次清洗；方案乙：分两次清洗．该物体初次清洗后受残留水等因素影响，其

质量变为a(1≤a≤3)．设用x单位质量的水初次清洗后的清洁度是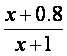(x＞a-1)，用

y单位质量的水第二次清洗后的清洁度是，其中c(0.8＜c＜0.99)是该物体初次清

洗后的清洁度．

(Ⅰ)分别求出方案甲以及c=0.95时方案乙的用水量，并比较哪一种方案用水量较少；

(Ⅱ)若采用方案乙，当a为某定值时，如何安排初次与第二次清洗的用水量，使总用水

量最少?并讨论a取不同数值时对最少总用水量多少的影响．

      解  (Ⅰ)设方案甲与方案乙的用水量分别为x与z，由题设有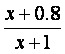=0.99，解得x=19．

由c=0.95得方案乙初次用水量为3，第二次用水量y满足方程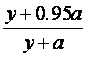=0.99，解得y=4a，故z=4a+3．

即两种方案的用水量分别为19与4a+3．

因为当1≤a≤3时，x-z=4(4-a)＞0，即x＞z．

故方案乙的用水量较少．

（Ⅱ）设初次与第二次清洗的用水量分别为x与y，类似（Ⅰ）得

x=，y=a（99-100c）      （*）

于是x+y=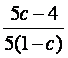+a（99-100c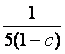）=+100a（1-c）-a-1.

当a为定值时，x+y≥2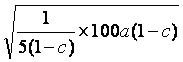-a-1=-a+4-1.

当且仅当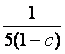=100a（1-c）时等号成立.此时c=1+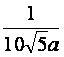（不合题意，舍去）

或c=1-∈（0.8，0.99）.

将c=1-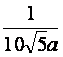代入（*）式得x=2-1＞a-1，y=2-a.

故c=1-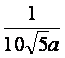时总用水量最小，此时第一次与第二次用水量分别为2-1与2-a，最少总用水量是T（a）=-a+4-1.

当1≤a≤3时，T′（a）=-1＞0，故T（a）是增函数（也可以用二次函数的单调性判断）.这说明，随着a的值的增加，最少总用水量增加.