|
23.2.4排序不等式<-->返回列表
数学归纳法
在证明一个与正整数有关的命题时,可采用下面两个步骤:
1 证明 时命题成立; 时命题成立;
2 证明:如果 时命题成立,那么 时命题成立,那么 时命题也成立。 时命题也成立。
我们有(1)(2)作依据,根据(1),知 时命题成立,再根据(2)知 时命题成立,再根据(2)知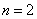 时命题成立,再依据(2)知 时命题成立,再依据(2)知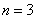 时命题成立,这样延续下去,就可以知道对任何正整数n命题成立,这种证明方法叫做数学归纳法。 时命题成立,这样延续下去,就可以知道对任何正整数n命题成立,这种证明方法叫做数学归纳法。
详解:
用数学归纳法证明一个与正整数有关的命题的步骤是:
1 证明当n取第一个值 (例如 (例如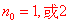 等)时结论正确; 等)时结论正确;
2 假设当 时结论正确,证明当 时结论正确,证明当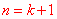 时结论正确。 时结论正确。
在完成这两个步骤后,可以判定命题对于从开始的所有正整数n都正确。
贝努利不等式
我们称不等式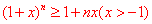 为贝努利不等式。 为贝努利不等式。
对于贝努利不等式的证明可以采用归纳法进行证明。
23.2.4排序不等式<-->返回列表
全网搜索"23.2.5数学归纳法与贝努利不等式"相关
|

