|
21.1.4直角三角形的射影定理<-->21.2.2圆内接四边形的性质与判定
21.2.1圆周角定理
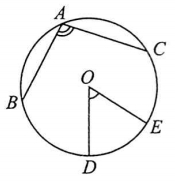
(1)圆周角的概念
顶点在圆上且两边都和圆相交的角叫做圆周角.如图,$\angle BAC$ 为圆周角,圆周角的范围是(0°,180°)
圆周角应满足两个条件:一是顶点在圆上;二是两边都与圆相交,二者缺一不可.
(2)圆心角的概念
顶点在圆心的角叫做圆心角.圆心角的度数等于它所对的弧的度数.如图,$\angle DOE$为圆心角.
圆心角一般是指劣弧所对的角,其范围是(0°,360°).
(3)圆周角定理
定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半,其度数等于它所对的弧的度数的一半.
相交弦所成角定理:圆的两条相交弦所成角的度数等于它所夹的弧与它的对顶角所夹弧的度数和的一半
推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
推论2:半圆(或直径)所对的圆周角是直角;
同圆或等圆中,两个圆心角、两条弧、两条弦的相等关系,
简单地说,就是圆心角相等↔弧相等↔弦相等
21.1.4直角三角形的射影定理<-->21.2.2圆内接四边形的性质与判定
全网搜索"21.2.1圆周角定理"相关
|

