|
17.2.2用样本的分布频率分布估计总体分布<-->17.2.4用样本标准差估计总体方差
17.2.3用样本的数字特征估计总体的数字特征
(1)总体特征数
能反映总体某种特征的量称为总体特征数
(2)众数、中位数、平均数
①众数:出现次数最多的数叫做众数。若有几个数据出现得最多,且出现的次数一样,这些数据都是这组数据的众数;若一组数中,每个数据出现的次数一样多,则认为这组数据没有众数。
②中位数:如果将一组数据按从小到大的顺序依次排列,当数据有奇数个时,处在最中间的一个数是这组数据的中位数;当数据有偶数个时,处在最中间的两个数的平均值是这组数据的中位数。
③平均数:一组数据的总和除以数据的个数所得的商就是平均数,记作: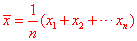 . .
详解:
(1)众数体现了样本数据的最大集中点,但它显然对其他数据信息的忽视使得无法客观地反映总体特征。
(2)中位数对极端值不敏感,仅利用中间数据的信息。
(3)平均数与每一个样本数据有关,能更多地反映关于样本数据全体的信息,但平均数受极端值影响大,使用平均数估计总体时,可靠性降低。 
【说明】(1)若有两个或几个数据出现得最多且出现的次数一样,这些数据都是这组数据的众数;若一组数据中,每个数据出现的次数一样多,则认为这组数据没有众数.
(2)由于平均数与每一个样本的数据有关,所以任何一个样本数据的改变都会引起平均数的改变,这是众数、中位数不具有的性质.也正因为这个原因,与众数、中位数比较起来,平均数可以反映出更多的关于样本数据全体的信息,但平均数受数据中的极端值的影响较大,使平均数在估计总体时可靠性降低.
(3)各数字特征的优缺点:众数体现了样本数据的最大集中点,但它对其他数据信息的忽视使得无法客观地反映总体特征;中位数是样本数据所占频率的等分线,它不受少数几个极端值的影响,这在某些情况下是优点,但它对极端值的不敏感有时也成为缺点.因为这些极端值有时是不能忽视的.
17.2.2用样本的分布频率分布估计总体分布<-->17.2.4用样本标准差估计总体方差
全网搜索"17.2.3用样本的数字特征估计总体的数字特征"相关
|

