|
返回列表<-->18.1.2程序框图
算法的概念
定义：在数学中，现在意义上的“算法”通常是指可以用计算机来解决的某一类问题的程序或步骤，这些程序或步骤必须是明确和有效的，而且能够在有限步之内完成。
算法的特点：
①有限性：一个算法的步骤序列是有限的，它应在有限步操作之后停止，而不能是无限的。②确定性：算法中的每一步都是确定的，并且能有效地执行且得到确定的结果，而不应当是模棱两可的。比如求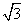 的近似值却没规定精确度，不同的同学会得到不同的结果，或者说该问题根本不能求解。③顺序性与正确性：算法从初始步骤开始，分为若干明确的步骤，每一个步骤只能有一个确定的后继步骤，前一步是后一步的前提，只有执行完前一步才能进行下一步，并且每一步都准确无误，才能解决问题。④不唯一性：求解某一个问题的算法不一定是唯一的，对于一个问题可以有不同的算法。⑤普遍性：很多具体的问题，都可以设计合理的算法去解决，如心算、计算器计算都要经过有限的、事先设计好的步骤加以解决。
详解：
学习算法的概念应注意以下三点：
1 算法并没有一个精确的定义，可以理解为基本运算及规定的运算顺序所构成的完整的集体步骤，或看成按要求设计好的有限的、确切的计算序列，并且这样的步骤或序列能够解决一类问题。
2 通俗点说，算法就是计算机解题的过程。在这个过程中，无论是形成的解题思路还是编写程序，都是在实施某种算法，前者是推理实现的算法，后者是操作实现的算法。
3 描述算法可以有不同的方式。例如，可以用自然语言和数学语言加以叙述，也可以用算法给出精确的说明，或者用框图直观地显示算法的全貌。
返回列表<-->18.1.2程序框图
全网搜索"18.1.1算法"相关
|
