|
10.1.2不等式建立的基础<-->10.1.4不等式性质的应用
①不等式性质定理
教材的叙述,不等式性质定理如下:
(1)a>b⇔b<a;
(2)a>b,b>c⇒a>c;
(3)a>b⇒a+c>b+c;
(4)a>b,c>d⇒a+c>b+d;
(5)a>b,c>0⇒ac>bc;a>b,c<0⇔ac<bc;
(6)a>b>0,c>d>0⇒ac>bd;
(7)a>b>0⇒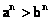 (n∈N,且n>1); (n∈N,且n>1);
(8)a>b>0⇒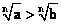 (n∈N,且n>1) (n∈N,且n>1)
②与等式性质比较

③不等式性质实质
不等式性质的实质是某些函数单调性的具体化。例如:

函数y=kx(k>0)在R上是增函数
∴若a>b,则ka>kb。
函数y=kx(k<0)在R上是减函数
∴若a>b,则ka<kb。

10.1.2不等式建立的基础<-->10.1.4不等式性质的应用
全网搜索"10.1.3不等式的性质"相关
|

