|
9.3.6等比数列前n项和公式的性质及简单应用<-->9.3.8等比数列求解与证明的基本方法
等比数列的图象
当q>1时,等比数列图象为:
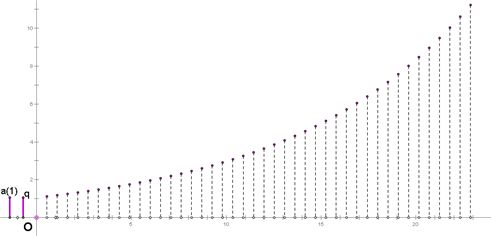
当q=1时,等比数列图象为:
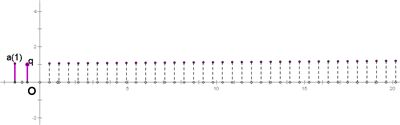
当0<q<1时,等比数列图象为:
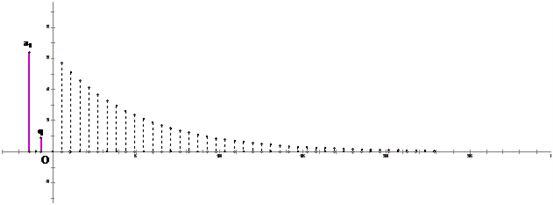
当q<0时,等比数列图象为:
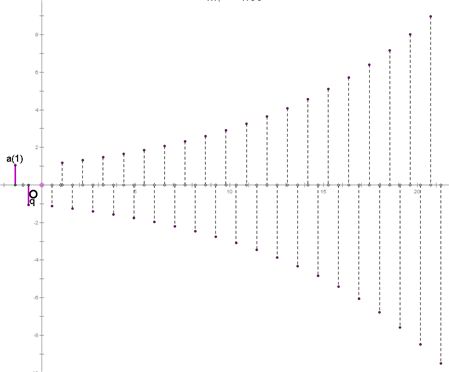
当q=-1时,等比数列图象为:
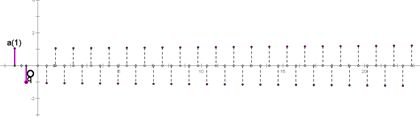
等比数列的性质
Ⅰ、函数性质:
(1)当a1 =1时,an =q n-1 ,an 是关于n的指数式,从图象上看,表示数列的各点(n,an )均在指数函数图象向右平移1个单位的函数y=qx-1 的图象上,具有相关指数函数的性质。
(2) 当a1 ≠1时,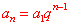 ,从图象上看,表示数列的各点(n,an )均在指数函数图象向右平移1个单位、纵向伸缩 ,从图象上看,表示数列的各点(n,an )均在指数函数图象向右平移1个单位、纵向伸缩 倍的函数 倍的函数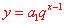 的图象上,具有变换的指数函数的相关性质。 的图象上,具有变换的指数函数的相关性质。
Ⅱ、运算性质:
(1)  、 、 是等比数列,则 是等比数列,则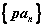 、 、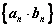 、 、 (其中p是非零常数、k是常数)也是等比数列。 (其中p是非零常数、k是常数)也是等比数列。
(2)  是正数等比数列,则 是正数等比数列,则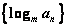 (其中是常数,m>0,m≠1)是等差数列。 (其中是常数,m>0,m≠1)是等差数列。
Ⅲ、等距离性质:
一、首末等距离
(1)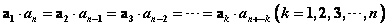 ; ;
(2)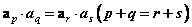 。 。
形象地: 对称(积)
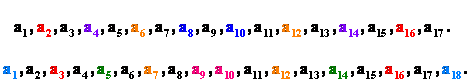
二、等间隔项等距离
等比数列的等间隔项仍然组成等比数列,仍然具有等距离的性质。
形象地:
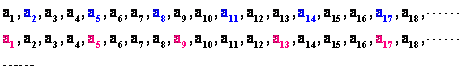
如,等比数列 ,则 ,则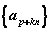 (其中p、k是常数, (其中p、k是常数,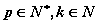 )仍然是等比数列。 )仍然是等比数列。
三、等间隔等长(和)等距离
等比数列的等间隔等项数的项之和仍然组成等比数列。
形象地:
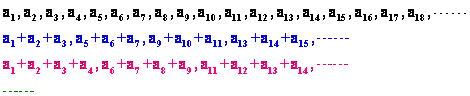
如,等比数列 ,则 ,则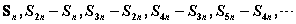 仍然是等比数列 仍然是等比数列
2.等比数列的性质:若 为等比数列,公比为 为等比数列,公比为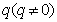 ,则 ,则
(1)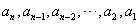 仍为等比数列,公比为 仍为等比数列,公比为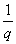 ; ;
(2)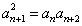 ; ;
(3)若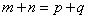 ,则 ,则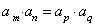 ,反之不一定成立。 ,反之不一定成立。
若 ,则 ,则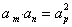
(4)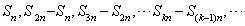 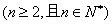 成等比数列,公比为 成等比数列,公比为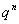 ; ;
(5)当n为偶数时,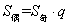 ;n为奇数时, ;n为奇数时,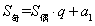
详解:
(1)非零常数列简记形式为 ,它既是等差数列(公差为0)又是等比数列(公比为1)。 ,它既是等差数列(公差为0)又是等比数列(公比为1)。
(2)等比数列中任一项都不取0,且公比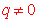 . .
9.3.6等比数列前n项和公式的性质及简单应用<-->9.3.8等比数列求解与证明的基本方法
全网搜索"9.3.7等比数列的性质"相关
|

