|
9.1.3数列的分类<-->9.1.5数列的递推公式
(1)数列的第$n$项叫做数列的通项,
(2)如果数列$\{a_n\}$的第$n$项与序号$n$之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.
注意!
①并不是所有的数列都有通项公式,如$π$的精确到$1,0.1,0.01,0.001,…$的不足近似值排成的数列:$3,3.1,3.14,3.141,…$就没有通项公式
②只给出一个数列的最初若干项,而未指明构成规律时,该数列的通项公式不能唯一地确定.例如,使数列$1,4,7,10,…$
前四项适合的通项公式可以是$a_n=3n-2$,也可以是
$a_n=1+3(n-1)+(n-1)(n-2)(n-3)(n-4)$
另外,数列通项公式的表示法也不是唯一的.如$a_n=\cos nπ$及$a_n=(-1)^n$均是数列$-1,1,-1,1,…$的通项公式.
数列通项公式的求法
⑴已知前n项—可用观察法,通常先将每项进行合理的等价变形,以便发现数列的项与项数n的关系,然后用不完全归纳法得出通项公式。
⑵已知 ,可用 ,可用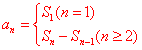
⑶已知首项 ,递推公式为 ,递推公式为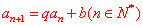 ,可构造数列 ,可构造数列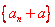 ,使其满足 ,使其满足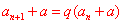 ,其中a可由待定系数法确定,即 ,其中a可由待定系数法确定,即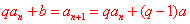   最后转化为可用累加、累乘或基本数列知识来解决的数列。 最后转化为可用累加、累乘或基本数列知识来解决的数列。
⑷已知 且 且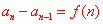 ,可用“累加法”。即 ,可用“累加法”。即
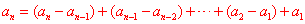
⑸已知 且 且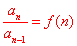 ,可用“累乘法” ,可用“累乘法”
即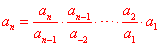
9.1.3数列的分类<-->9.1.5数列的递推公式
全网搜索"9.1.4数列的通项公式"相关
|

