|
8.1.3向量的模<-->8.1.5向量概念的错判辨析
单位向量
〖定义〗长度等于1个单位的向量。
零向量
〖定义〗长度为0的向量,即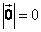 。 。
详解:
〖概念辨析〗
1、由于零向量是特殊的向量,方向看作是任意的,规定零向量与任意方向的向量平行,即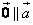 . .
2、书写时,一定要记得加箭号,否则就成数字0了。
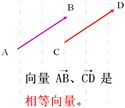
相等向量
〖定义〗相等向量:长度相等且方向相同的向量叫做相等向量。
〖代数表示〗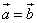 , ,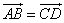
〖几何表示〗
详解:
〖概念辨析〗两个向量只有当它们的模相等,同时方向相同时,才能称它们相等。相等的向量可以认为是“同一”向量。
共线向量
〖定义〗共线向量(平行向量):方向相同或相反的非零向量,
〖代数表示〗
〖几何表示〗如图
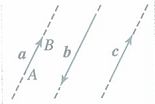
详解:
〖概念辨析〗
1、向量是可以平移的,任意一组共线向量都可以移到同一直线上。
2、共线向量也就是平行向量,其要求是几个非零向量的方向相同或相反,当然向量所在的直线可以平行,也可以重合,其中“共线”的含义不是平面几何中“共线”的含义,实际上,共线向量有以下四种情况:
a、方向相同且模相等;
b、方向相同且模不等;
c、方向相反且模相等;
d、方向相反且模不等。
3、共线向量不一定是相等向量,而相等向量一定是共线向量。
8.1.3向量的模<-->8.1.5向量概念的错判辨析
全网搜索"8.1.4与向量有关的概念"相关
|

