|
4.3.8求函数的最大值与最小值的步骤<-->4.4.1定积分
生活中经常遇到求利润最大、用料最省、效率最高等问题,这些问题通常称为优化问题.
解决优化问题的方法很多,如:判别式法、均值不等式法、线性规划法及利用二次函数的性质等.
不少优化问题,可以化为求函数最值问题.导数方法是解这类问题的有效工具.
(1)利用导数解决生活中的优化问题的一般步骤
①分析实际问题中各量之间的关系,列出实际问题的数学模型,写出实际问题中变量之间的函数关系$y=f(x)$;
②求函数的导函数$f'(x)$,解方程$f'(x)=0$;
③比较函数在区间端点和使$f'(x)=0$的点的数值的大小,最大(小)者为最大(小)值
(2)解决生活中的优化问题应当注意的问题
①在求实际问题的最大(小)值时,一定要考虑实际问题的意义,不符合实际意义的值应舍去;
②在实际问题中,有时会遇到函数在区间内只有一个点$f'(x)=0$的情形.如果函数在这点有极大(小)值,那么不与端点比较,也可以知道这就是最
大(小)值;
③在解决实际优化问题时,不仅要注意将问题中涉及的变量关系用函数关系表示,还应确定出函数关系式中自变量的定义区间.
(3)解决优化问题的基本思路
在解决实际优化问题时,我们不难发现,解决优化问题的基本思路是:
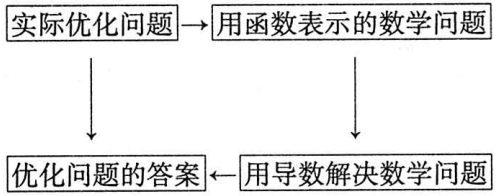
上述解决优化问题的过程是一个典型的数学建模过程。
4.3.8求函数的最大值与最小值的步骤<-->4.4.1定积分
全网搜索"4.3.9生活中的优化问题"相关
|

