|
4.1.2瞬时速度<-->4.1.4导数
(1)曲线$y=f(x)$在一点$P(x_0,y_0)$的切线概念
一般地,过曲线$y=f(x)$上一点$P(x_0,y_0)$作曲线的割线PQ,当Q点沿着曲线无限趋近于P时,若割线 PQ趋近于某一确定的位置,则称这一确定位置的直线为曲线$y=f(x)$在点P处的切线,如图
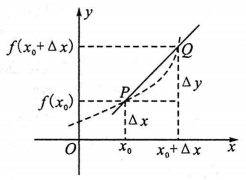
①与点P的位置有关.
②要依据割线 PQ是否存在极限位置来判定与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线.
(2)求曲线$y=f(x)$上一点$P(x_0,y_0)$处的切线(点P在曲线上且为切点)
先求出曲线$y=f(x)$上点P处的切线的斜率即$f'(x_0)$(可利用定义,也可求出$f'(x)$后代人$x$求$f'(x_0)$),再根据点斜式写出切线方程:$y-y_0=f'(x_0)(x-x_0)$.
(3)求曲线$y=f(x)$的过点$P(x_0,y_0)$的切线
设切点坐标为$(x_1,f(x_1))$,利用$f'(x_1)=\dfrac{f(x_1)-y_0}{x_1-x_0}$求得$x_0$,得到切点坐标及$f'(x)$,再根据点斜式写出切线方程:$y-y_1=f'(x_1)(x-x_1)$.
注意!对于(3)中的情况,点P可能不在曲线上,或P在曲线上但不一定为切点,如$f(x)=x3$.
4.1.2瞬时速度<-->4.1.4导数
全网搜索"4.1.3曲线的切线"相关
|

