|
2024年高考数学上海19<-->2024年高考数学上海21
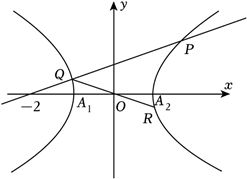
(18分)已知双曲线$\Gamma :x^2-\dfrac{y^2}{b^2}=1$,$(b > 0)$,左右顶点分别为$A_{1}$,$A_{2}$,过点$M(-2,0)$的直线$l$交双曲线$\Gamma$于$P$、$Q$两点,且点$P$在第一象限.
(1)当离心率$e=2$时,求$b$的值;
(2)当$b=\dfrac{2\sqrt{6}}{3}$,△$MA_{2}P$为等腰三角形时,求点$P$的坐标;
(3)连接$OQ$并延长,交双曲线$\Gamma$于点$R$,若$\overrightarrow{A_1R}\cdot \overrightarrow{A_2P}=1$,求$b$的取值范围.
答案:(1)$b=\sqrt{3}$;
(2)$P(2,2\sqrt{2})$;
(3)$b\in (0,\sqrt{3})\bigcup (\sqrt{3},\dfrac{\sqrt{30}}{3}]$.
分析:(1)由题意可得$\dfrac{c}{a}=2$,$a=1$,可得$c=2$,由$a^{2}+b^{2}=c^{2}$求解即可;
(2)由题意可得$MA_{2}=PA_{2}$,$P(x_{0}$,$y_{0})$,$x_{0} > 0$,$y_{0} > 0$,则可得$(x_0-1)^2+y_0^2=9$,再由$x_0^2-\dfrac{y_0^2}{\dfrac{8}{3}}=1$,求解即可;
(3)设$P(x_{1}$,$y_{1})$ $Q(x_{2}$,$y_{2})$ 则$R(-x_{2}$,$-y_{2})$,设直线$l:x=my-2(m > \dfrac{1}{b})$,联立直线与双曲线方程,再结合韦达定理可得$y_{1}+y_{2}=\dfrac{4{b}^{2}m}{{b}^{2}{m}^{2}-1}$,$y_{1}y_{2}=\dfrac{3{b}^{2}}{{b}^{2}{m}^{2}-1}$,又由$\overrightarrow{A_1R}\cdot \overrightarrow{A_2P}=1$,得$(-x_{2}+1)(x_{1}-1)-y_{1}y_{2}=1$,即有$(m^{2}+1)y_{1}y_{2}-3m(y_{1}+y_{2})+10=0$,可得$m^2=\dfrac{10-3b^2}{b^2} > \dfrac{1}{b^2}$,即可得答案.
解:(1)因为$e=2$,即$\dfrac{c}{a}=2$,
所以$\dfrac{c^2}{a^2}=4$,
又因为$a^{2}=1$,
所以$c^{2}=4$,
又因为$a^{2}+b^{2}=c^{2}$,
所以$b^{2}=3$,
所以$b=\sqrt{3}$(负舍);
(2)因为△$MA_{2}P$为等腰三角形,
①若$A_{1}A_{2}$为底,则点$P$在线段$MA_{2}$的中垂线,即$x=-\dfrac{1}{2}$上,与$P$双曲线上且在第一象限矛盾,故舍去;
②若$A_{2}P$为底,则$MP=MA_{2}$,与$MP > MA_{2}$矛盾,故舍去;
③若$MP$为底,则$MA_{2}=PA_{2}$,
设$P(x_{0}$,$y_{0})$,$x_{0} > 0$,$y_{0} > 0$,
则$\sqrt{(x_0-1)^2+(y_0-0)^2}=3$,
即$(x_0-1)^2+y_0^2=9$,
又因为$x_0^2-\dfrac{y_0^2}{\dfrac{8}{3}}=1$,
得$(x_0-1)^2+(x_0-1)^2\times \dfrac{8}{3}=9$,
得$11x_0^2-6x_0-32=0$,
解得$x_0=2,y_0=2\sqrt{2}$,
即$P(2,2\sqrt{2})$;
(3)由$A_{1}(-1,0)$,设$P(x_{1}$,$y_{1})$,$Q(x_{2}$,$y_{2})$,
则$R(-x_{2}$,$-y_{2})$,设直线$l:x=my-2(m > \dfrac{1}{b})$,
联立$\left\{\begin{array}{l}{x=my-2}\\ {{x}^{2}-\dfrac{{y}^{2}}{{b}^{2}}=1}\\ {m > \dfrac{1}{b}}\end{array}\right.$,得$(b^{2}m^{2}-1)y^{2}-4b^{2}my+3b^{2}=0$,
则$y_{1}+y_{2}=\dfrac{4{b}^{2}m}{{b}^{2}{m}^{2}-1}$,$y_{1}y_{2}=\dfrac{3{b}^{2}}{{b}^{2}{m}^{2}-1}$,
所以$\overrightarrow{{A}_{1}R}=(-x_{2}+1$,$-y_{2})$,$\overrightarrow{{A}_{2}P}=(x_{1}-1$,$y_{1})$,
又因为$\overrightarrow{A_1R}\cdot \overrightarrow{A_2P}=1$,
得$(-x_{2}+1)(x_{1}-1)-y_{1}y_{2}=1$,
则$(x_{2}-1)(x_{1}-1)+y_{1}y_{2}=-1$,
即$(my_{2}-3)(my_{1}-3)+y_{1}y_{2}=-1$,
化简后可得到$(m^{2}+1)y_{1}y_{2}-3m(y_{1}+y_{2})+10=0$,
再由韦达定理得$3b^{2}(m^{2}+1)-12m^{2}b^{2}+10(b^{2}m^{2}-1)=0$,
化简得$b^{2}m^{2}+3b^{2}-10=0$,
所以$m^2=\dfrac{10}{b^2}-3$,代入$b^{2}m^{2}-1\ne 0$,得$b^{2}=10-3b^{2}\ne 1$,所以$b^{2}\ne 3$,
且$m^2=\dfrac{10}{b^2}-3\geqslant 0$,解得$b^2\leqslant \dfrac{10}{3}$,
又因为$b > 0$,则$0 < b^2\leqslant \dfrac{10}{3}$,
综上,$b^2\in (0,3)\bigcup (3,\dfrac{10}{3}]$,
$b\in (0,\sqrt{3})\bigcup (\sqrt{3},\dfrac{\sqrt{30}}{3}]$.
点评:本题考查了双曲线的性质、直线与双曲线的位置关系及韦达定理的应用,属于中档题.
2024年高考数学上海19<-->2024年高考数学上海21
全网搜索"2024年高考数学上海20"相关
|

