|
2023年高考数学新高考Ⅱ-15<-->2023年高考数学新高考Ⅱ-17
(5分)已知函数$f(x)=\sin (\omega x+\varphi )$,如图,$A$,$B$是直线$y=\dfrac{1}{2}$与曲线$y=f(x)$的两个交点,若$\vert AB\vert =\dfrac{\pi }{6}$,则$f(\pi )=$ $-\dfrac{\sqrt{3}}{2}$ .
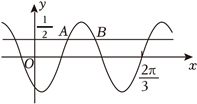
分析:由$A$,$B$两点的位置入手,结合整体代换思想,先确定$\omega$,再根据图象的位置,找出合乎条件的一个$\varphi$值,即可求解.
解:由题意:设$A(x_{1}$,$\dfrac{1}{2})$,$B(x_{2}$,$\dfrac{1}{2})$,则$x_{2}-x_{1}=\dfrac{\pi }{6}$,
由$y=A\sin (\omega x+\varphi )$的图象可知:
$\omega x_{2}+\varphi -(\omega x_{1}+\varphi )=\dfrac{5\pi }{6}-\dfrac{\pi }{6}=\dfrac{2\pi }{3}$,即$\omega (x_{2}-x_{1})=\dfrac{2\pi }{3}$,
$\therefore \omega =4$,
又$f(\dfrac{2\pi }{3})=\sin (\dfrac{8\pi }{3}+\varphi )=0$,$\therefore$$\dfrac{8\pi }{3}+\varphi =k\pi$,$k\in Z$,
即$\varphi =-\dfrac{8\pi }{3}+k\pi$,$k\in Z$,
观察图象,可知当$k=2$时,$\varphi =-\dfrac{2\pi }{3}$满足条件,
$\therefore f(\pi )=\sin (4\pi -\dfrac{2\pi }{3})=-\dfrac{\sqrt{3}}{2}$.
故答案为:$-\dfrac{\sqrt{3}}{2}$.
点评:本题主要考查根据函数$y=A\sin (\omega x+\varphi )$的图象确定解析式的方法,属中档题.
2023年高考数学新高考Ⅱ-15<-->2023年高考数学新高考Ⅱ-17
全网搜索"2023年高考数学新高考Ⅱ-16"相关
|

