|
2023年高考数学甲卷-文17<-->2023年高考数学甲卷-文19
(12分)如图,在三棱柱$ABC-A_{1}B_{1}C_{1}$中,$A_{1}C\bot$平面$ABC$,$\angle ACB=90^\circ$.
(1)证明:平面$ACC_{1}A_{1}\bot$平面$BB_{1}C_{1}C$;
(2)设$AB=A_{1}B$,$AA_{1}=2$,求四棱锥$A_{1}-BB_{1}C_{1}C$的高.
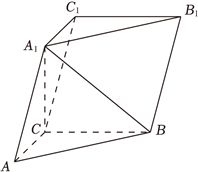
答案:(1)证明见解答;
(2)四棱锥$A_{1}-BB_{1}C_{1}C$的高为1.
分析:(1)根据线面垂直,面面垂直的判定与性质定理可得平面$ACC_{1}A_{1}\bot$平面$BB_{1}C_{1}C$;
(2)利用已知可得$A_{1}C=AC$,进而可得$A_{1}C=AC=\sqrt{2}$,过$A_{1}$作$A_{1}O\bot C_{1}C$于$O$,可得$A_{1}O$为四棱锥$A_{1}-BB_{1}C_{1}C$的高,求解即可.
解:(1)$\because A_{1}C\bot$底面$ABC$,$BC\subset$面$ABC$,
$\therefore A_{1}C\bot BC$,又$BC\bot AC$,$A_{1}C$,$AC\subset$平面$ACC_{1}A_{1}$,$A_{1}C\bigcap AC=C$,
$\therefore BC\bot$平面$ACC_{1}$,又$BC\subset$平面$BCC_{1}B_{1}$,
$\therefore$平面$ACC_{1}A_{1}\bot$平面$BCC_{1}B_{1}$;
(2)$\because BC\bot$平面$ACC_{1}$,$AC$,$A_{1}C\subset$平面$ACC_{1}$,
$\therefore BC\bot AC$,$BC\bot A_{1}C$,
$\because AB=A_{1}B$,$BC=BC$,
$\therefore \rm{Rt}\Delta ABC\cong Rt$△$A_{1}BC$,
$\therefore A_{1}C=AC$,
$\because A_{1}C\bot$底面$ABC$,$AC\subset$面$ABC$,
$\therefore A_{1}C\bot AC$,$\therefore A_{1}C^{2}+AC^{2}=A_{1}A^{2}$,
$\because AA_{1}=2$,$\therefore A_{1}C=AC=\sqrt{2}$,
$\therefore A_{1}C_{1}=\sqrt{2}$,
过$A_{1}$作$A_{1}O\bot C_{1}C$于$O$,$\because A_{1}C=A_{1}C_{1}$,
$\therefore O$为$CC_{1}$的中点,$\therefore A_{1}O=\dfrac{1}{2}C_{1}C=\dfrac{1}{2}A_{1}A=1$,
由(1)可知$A_{1}O\bot$平面$BCC_{1}B_{1}$,
$\therefore$四棱锥$A_{1}-BB_{1}C_{1}C$的高为1.
点评:本题考查面面垂直的证明,考查四棱锥的高的求法,属中档题.
2023年高考数学甲卷-文17<-->2023年高考数学甲卷-文19
全网搜索"2023年高考数学甲卷-文18"相关
|

