(1)$f(p)=\text{C}_{20}^2 p^2(1-p)^{18}$,
$f'(p)=\text{C}_{20}^2 [2p(1-p)^{18}-18p^2(1-p)^{17}$
$=\text{C}_{20}^2 (1-p)^{17}2p(1-10p)$,$0<p<1$,
当$p=\dfrac{1}{10}$时,$f'(p)=0$,且$f'(p)$在$(0,\dfrac{1}{10})$上时$f'(p)>0$,在$(\dfrac{1}{10},1)$上时$f'(p)<0$,
所以当$p=\dfrac{1}{10}$时,$f(p)$取最大值,
$f(p)$的最大值为$f(\dfrac{1}{10})=\dfrac{19 \times 9^{18}}{10^{19}}$,
即$f(p)$的最大值点$p_0=0.1$。
(2)(i)该分布本质上为二项分布,
设一箱产品花的费用为$X$,
则其分布如下图,
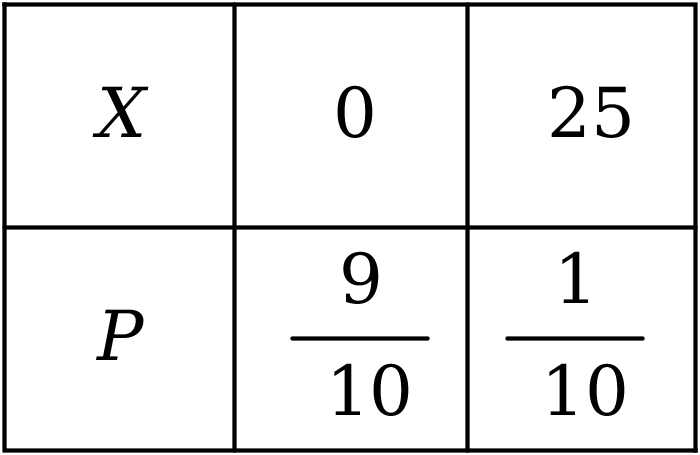
$EX=np+20 \times 2=25 \times 180 \times \dfrac{1}{10}+40=490$,
(ii)若验证花费$200 \times 2 =400$元,需验证。

