| 2022年高考数学乙卷-文8 |
|
2022-12-16 17:36:33 |
|
|
(5分)如图是下列四个函数中的某个函数在区间$[-3$,$3]$的大致图像,则该函数是( )
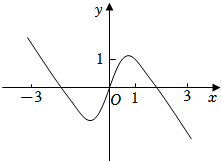
A.$y=\dfrac{-{x^3}+3x}{{x^2}+1}$ B.$y=\dfrac{{x^3}-x}{{x^2}+1}$
C.$y=\dfrac{2x\cos x}{{x^2}+1}$ D.$y=\dfrac{2\sin x}{{x}^{2}+1}$
分析:首先分析函数奇偶性,然后观察函数图像在$(1,3)$存在零点,可排除$B$选项,再利用基本不等式可判断$CD$选项错误.
解:首先根据图像判断函数为奇函数,
其次观察函数在$(1,3)$存在零点,
而对于$B$选项:令$y=0$,即$\dfrac{{x}^{3}-x}{{x}^{2}+1}=0$,解得$x=0$,或$x=1$或$x=-1$,故排除$B$选项;
$C$选项:当$x > 0$时,$2x > 0$,$x^{2}+1 > 0$,因为$\cos x\in [-1$,$1]$,故$\dfrac{2x\cos x}{{x}^{2}+1}\leqslant \dfrac{2x}{{x}^{2}+1}=\dfrac{2}{x+\dfrac{1}{x}}$,且当$x > 0$时,$x+\dfrac{1}{x}\geqslant 2$,故$\dfrac{2}{x+\dfrac{1}{x}}\leqslant 1$,而观察图像可知当$x > 0$时,$f(x)_{max}\geqslant 1$,故$C$选项错误.
同理$D$选项,$x^{2}+1 > 0$,$\sin x\in [-1$,$1]$,$\dfrac{2\sin x}{{x}^{2}+1}\leqslant \dfrac{2}{{x}^{2}+1}$,当$x > 0$时,$x+\dfrac{1}{x}\geqslant 2$,故$\dfrac{2}{x+\dfrac{1}{x}}\leqslant 1$,故排除$D$选项;
故选:$A$.
点评:本题主要考查函数图像的识别,属于基础题.
|
|
http://x.91apu.com//shuxue/gkt/2022/2022qgyw/2022-12-16/33498.html |

