14.3.6利用向量方法求空间距
空间中的距离有:点与点的距离、点到线的距离、点到面的距离、线与线的距离、线与面的距离、面与面的距离.
(1)点面距离的求法

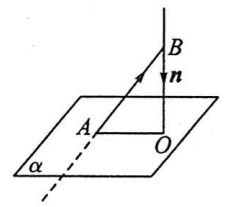
如图,$BO \bot 平面 α$,垂足为$O$,则点$B$到平面$α$的距离就是线段 $BO$ 的长度
若$AB$是平面$α$的任一条斜线段，则在$Rt\triangle BOA$中，
$|\vec{BO}|=|\vec{BA}|\cdot \cos \angle ABO= \dfrac{|\vec{BA}| \cdot |\vec{BO}|\cdot \cos \angle ABO}{|\vec{BO}|}$

如果令平面α的法向量为",考虑到法向量的方向
可以得到$B$点到平面$α$的距离为$|\vec{BO}|=\dfrac{|\vec{AB}·\vec{n}|}{|\vec{n}|}$

因此要求一个点到平面的距离,可以分以下几步完成:
①求出该平面的一个法向量;
②找出从该点出发的平面的任一条斜线段对应的向量;
③求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即可求出点到平面的距离线面距、面面距均可转化为点面距离，用求点面距的方法进行求解，
(2)两异面直线距离的求法(*)

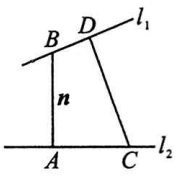
如图 ,设$l_1,l_2$是两条异面直线,$\vec{n}$是$l_1$与$l_2$的公垂线段 $AB$的方向向量,又$C,D$分别是$l_1,l_2$上的任意两点,则$l_1$与$l_2$的距离是 $d=|\vec{AB}|=\dfrac{|\vec{CD}\cdot \vec{n}|}{|\vec{n}|}$

(3)空间中各种距离一般都可以转化为点点距、点线距、点面距,其中点点距、点线距最终都可用空间向量的模来求解,而点面距则可由平面的法向量来求解.