14.3.5利用向量求空间角
(1)求异面直线所成的角
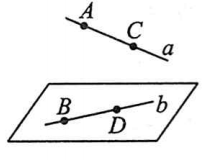
已知$a,b$为两异面直线$A,C$与$B,D$分别是$a,b$上的任意两点,$a,b$所成的角为$\theta$,则
$\cos \theta =\dfrac{|\vec{AC}\cdot \vec{BD}|}{|\vec{AC}|\cdot |\vec{BD}|}$

注意!
两异面直线所成的角可以通过这两条直线的方向向量的夹角来求得,但二者不完全相等，当两方向向量的夹角是钝角时,应取其补角作为两异面直线所成的角.
(2)求直线和平面所成的角

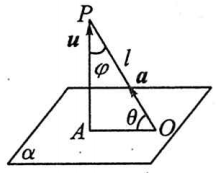
设直线$l$的方向向量为$\vec{a}$，平面$α$的法向量为$\vec{u}$,直线与平面所成的角为$\theta$,$\vec{a}$与$\vec{u}$的夹角为$\varphi$,则有
$\sin \theta =|\cos \varphi|=\dfrac{|\vec{a}\cdot \vec{u}|}{|\vec{a}|\cdot |\vec{u}|}$
此外可由定义得到直线与平面所成的角$\theta$,如图$\theta  =\angle POA = <\vec{OP},\vec{OA} > $

(3)求二面角

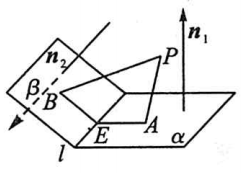
如图,若$PA \bot α$于$A$,$PB \bot B$于$B$,平面$PAB$交$l$于$E$,则$\angle AEB为$二面角$\alpha-l-\beta$的平面角，$\angle AEB+\angle APB=180°$.
若$\vec{n_1}·\vec{n_2}$分别为面$α,\beta$的法向量,$\angle AEB= <\vec{n_1},\vec{n_2}>$或$(π-<\vec{n_1},\vec{n_2}>)$,即二面角$\theta$等于它的两个面的法向量的夹角(或夹角的补角)，
于是$\cos θ=\dfrac{\vec{n_1}\cdot \vec{n_1}}{|\vec{n_1}|\cdot |\vec{n_2}|}$
①当法向量$\vec{n_1}$与$\vec{n_2}$的方向分别指向二面角的内侧与外侧时,二面角$\theta$的大小等于法向量$\vec{n_1}，\vec{n_2}$
的夹角$< \vec{n_1},\vec{n_2} >$的大小.
2当法向量$\vec{n_1}$,$\vec{n_2}$的方向同时指向二面角的内侧或外侧时,二面角$\theta$的大小等于法向量$\vec{n_1}$,$\vec{n_2}$的夹角的补角$ π-<\vec{n_1},\vec{n_2}>$的大小.