|
异面直线:
①异面直线的定义:指不同在任何一个平面内的两条直线。
②异面直线的画法:作图时通常用一个或两个平面衬托。如图:

③异面直线的判定:本教材没有异面直线的判定定理,一般用反证法证明。
④异面直线所成的角:
Ⅰ、定义:如图所示,已知两条异面直线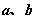 ,经过空间任一点O作直线 ,经过空间任一点O作直线 , , ,我们把 ,我们把 与 与 所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)。 所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)。

两条异面直线所成角的范围是(0°,90°]。
如果两条异面直线所成的角是直角,那么我们就说这两条异面直线互相垂直。两条互相垂直的异面直线a,b,记作 . .
Ⅱ、定义的实质:空间异面直线所成角化归转化为平面内两直线所成角来表示,体现了空间归面的思想方法。
Ⅲ、异面直线所成角的求法:平移归面法;向量法。
IV、两异面直线所成的角注意:
(1)两异面直线所成的角与点O的选取无关。
(2)两异面直线所成角θ的范围是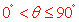 . .
(3)判定空间两条直线是异面直线的方法:
①判定定理:平面外一点A与平面内一点B连成的直线与平面内不过点B的直线是异面直线。
②反证法:证明两直线共面不可能。
|

