诱导公式成因
〖形成〗
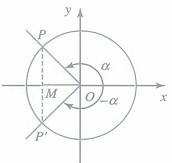
任意角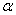
的终边与角
的终边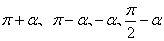具有某种对称关系。
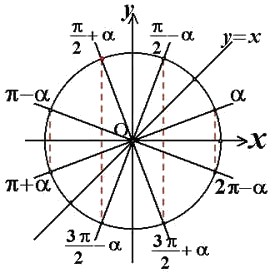
角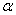的终边与角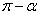
终边关于y轴对称，正弦值相等，其余值互为相反数；
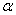角的终边与角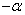
终边关于x轴对称，余弦值相等，其余值互为相反数；
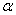角的终边与角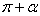
终边关于原点对称，正切值相等，其余值互为相反数；
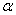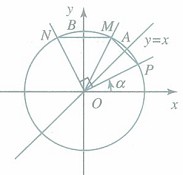
角的终边与角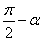
终边关于直线y=x对称，互余角的正余弦值相等
详解：
〖概念辨析〗诱导公式本质上是对称性的应用。
〖相关知识〗诱导公式
诱导公式一
〖公式〗：
；
；
；
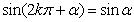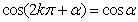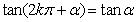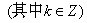诱导公式二
〖公式〗
；
；
；
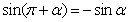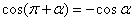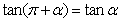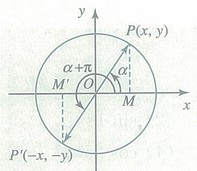
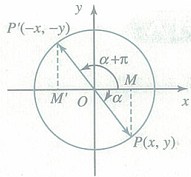
详解：
〖记忆方法〗符号看象限——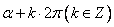
,
,
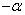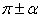的三角函数值等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号。
〖相关知识〗诱导公式成因
诱导公式三
〖公式〗
；
；
；
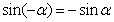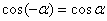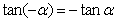详解：
〖记忆方法〗符号看象限——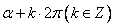
,
,
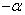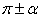的三角函数值等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号。
〖相关知识〗诱导公式成因
诱导公式四
〖公式〗
；
；
；
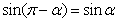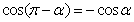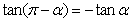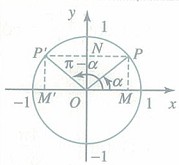
详解：
〖记忆方法〗符号看象限——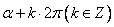
,
,
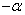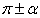的三角函数值等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号。
〖相关知识〗诱导公式成因
诱导公式五〖公式〗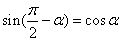
；
；
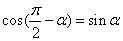
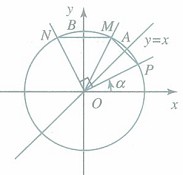
详解：
〖记忆方法〗符号看象限——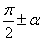
的正弦（余弦）函数值，分别等于α的余弦（正弦）函数值，前面加上一个把α看成锐角时原函数值的符号。
〖相关知识〗诱导公式成因
诱导公式六〖公式〗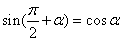
；
；
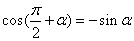
详解：
〖记忆方法〗符号看象限——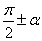
的正弦（余弦）函数值，分别等于α的余弦（正弦）函数值，前面加上一个把α看成锐角时原函数值的符号。
〖相关知识〗诱导公式成因
诱导公式应用步骤
〖步骤〗利用诱导公式把任意角的三角函数化为锐角三角函数的基本步骤是：
任意角的三角函数→正角的三角函数→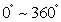
的三角函数→锐角三角函数。
〖图示〗
详解：
〖记忆方法〗先正再缩，终化锐——先把角转化为正角，然后把角的范围缩小到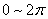
，最终化为锐角解决。
〖相关知识〗诱导公式成因
,
,
的三角函数值等于